Question

Prove that if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.

Using the above theorem prove that a line through the point of intersection of the diagonals and parallel to the base of the trapezium divides the non-parallel sides in the same ratio.

Answer 1

For the Theorem:

Given, To prove, Construction and figure

Proof

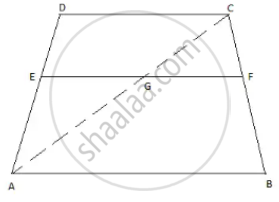
Let ABCD be a trapezium DC ∥ AB and EF is a line parallel to AB and hence to DC.

To prove: `(DE)/(EA) = (CF)/(FB)`

Construction: Join AC, meeting EF in G.

Proof: In ΔABC, we have

GF || AB

`(CG)/(GA) = (CF)/(FB)` [By BPT]  ......(1)

In ΔADC, we have

EG ∥ DC  .....(EF ∥AB and AB ∥ DC)

`(DE)/(EA) = (CG)/(GA)` [By BPT] ......(2)

From (1) and (2), we get,

`(DE)/(EA) = (CF)/(FB)`