Advertisements
Advertisements
प्रश्न
Figure shows Δ KLM , P an T on KL and KM respectively such that∠ KLM =∠ KTP.
If `"KL"/"KT" = 9/5` , find `("Ar" triangle "KLM")/("Ar" triangle "KTP")`.

उत्तर
Given : `"KL"/"KT"= 9/5`
To find : `("Ar" triangle "KLM")/("Ar" triangle "KTP")`
Sol : In Δ KLM and Δ KTP
∠ KLM =∠ KTP ....(Given)
∠ LKM = ∠ TKP ....(common)
Δ KLM and Δ KTP ......(AA corollary)
`therefore ("Ar" triangle "KLM")/("Ar" triangle "KTP") = ("KL"/"KT")^2 = (9/5)^2 = 81/25`
i.e., 81 : 25
[The ration of areas of two similar triangle is equal to the ratio of square of their corresponding sides.]
APPEARS IN
संबंधित प्रश्न
In the figure, given below, the medians BD and CE of a triangle ABC meet at G. Prove that:

- ΔEGD ~ ΔCGB and
- BG = 2GD from (i) above.
The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5cm, find the length of QR.
The corresponding altitudes of two similar triangles are 6cm and 9cm respectively. Find the ratio of their areas.
In Δ ABC, DE || BC; DC and EB intersects at F. if `"DE"/"BC" = 2/7` , find `("Ar" (triangle "FDE"))/("Ar" (triangle "FBC"))`
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 8cm, AB = 12cm and AE = 12cm, find CE.
In ΔABC, MN is drawn parallel to BC. If AB = 3.5cm, AM : AB = 5 : 7 and NC = 2cm, find:
(i) AM
(ii) AC
In the given figure, PB is the bisector of ABC and ABC =ACB. Prove that:
a. BC x AP = PC x AB
b. AB:AC = BP: BC
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆RPN

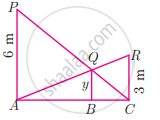
Two vertical poles of heights 6 m and 3 m are erected above a horizontal ground AC. Find the value of y

In ΔABC, DE || BC (as shown in the figure), If AD = 4 cm, AB = 9 cm and AC = 13.5 cm, then the length of EC is ______.
