Advertisements
Advertisements
प्रश्न
In ΔABC, MN is drawn parallel to BC. If AB = 3.5cm, AM : AB = 5 : 7 and NC = 2cm, find:
(i) AM
(ii) AC
उत्तर
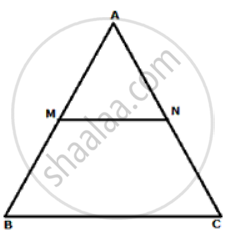
(i) `"AM"/"AB" = (5)/(7)`
∵ AB = 3.5cm
∴ AM = `(5 xx "AB")/(7)`
⇒ AM = `(5 xx 3.5)/(7)`
⇒ AM = 2.5cm.
(ii) Since MN || BC and `"AM"/"MB" = "AN"/"NC"`
∵ AB = 3.5cm; AM = 2.5cm
∴ MB
= AB - AM
= 3.5 - 2.5
= 1cm
⇒ `"AM"/"MB" = "AN"/"NC"`
⇒ `(2.5)/(1) = "AN"/(2)`
⇒ AN = `(2.5 xx 2)/(1)` = 5cm
Now,
AC = AN + NC
⇒ AC
= 5 + 2
= 7cm.
APPEARS IN
संबंधित प्रश्न
The diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the side BC. Prove that DF × EF = FB × FA
In triangle ABC, AD is perpendicular to side BC and AD2 = BD × DC. Show that angle BAC = 90°.
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3 : 5,

Find:
- ∆APB : ∆CPB
- ∆DPC : ∆APB
- ∆ADP : ∆APB
- ∆APB : ∆ADB
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

In the given figure, if ∠ADE = ∠B, show that ΔADE ~ ΔABC. If AD = 3.8cm, AE = 3.6cm, BE = 2.1cm and BC = 4.2cm, find DE.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : OA, if OA' = 6 cm.
A model of a ship is made to a scale 1 : 300.
- The length of the model of the ship is 2 m. Calculate the length of the ship.
- The area of the deck of the ship is 180,000 m2. Calculate the area of the deck of the model.
- The volume of the model is 6.5 m3. Calculate the volume of the ship.
In the following figure, point D divides AB in the ratio 3 : 5. Find :
DE = 2.4 cm, find the length of BC.

If ΔABC, D and E are points on AB and AC. Show that DE || BC for each of the following case or not:
AD = 5.7cm, BD = 9.5cm, AE = 3.3cm, and EC = 5.5cm
Given that ΔABC ∼ ΔPRQ, name the corresponding angles and the corresponding sides.
