Advertisements
Advertisements
प्रश्न
Two vertical poles of heights 6 m and 3 m are erected above a horizontal ground AC. Find the value of y
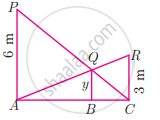
उत्तर
In the ∆PAC and ∆BQC
∠PAC = ∠QBC = 90°
∠C is common
∆PAC ~ QBC
`"AP"/"BQ" = "AC"/"BC"`
`6/y = "AC"/"BC"`
∴ `"BC"/"AC" = y/6` ...(1)
In the ∆ACR and ∆QBC
∠ACR = ∠QBC = 90°
∠A is common
∆ACR ~ ABQ
`"RC"/"QB" = "AC"/"AB"`
`3/y = "AC"/"AB"`
`"AB"/"AC" = y/3` ...(2)
By adding (1) and (2)
`"BC"/"AC" + "AB"/"AC" = y/6 + y/3`
1 = `(3y + 6y)/18`
9y = 18 ⇒ y = `18/9` = 2
The Value of y = 2 m
APPEARS IN
संबंधित प्रश्न
In figure, `\frac{AO}{OC}=\frac{BO}{OD}=\frac{1}{2}` and AB = 5 cm. Find the value of DC.
P and Q are points on sides AB and AC respectively of ∆ABC. If AP = 3 cm, PB = 6cm. AQ = 5 cm and QC = 10 cm, show that BC = 3PQ.
Given `triangle ABC ~ triangle PQR`, if `(AB)/(PQ) = 1/3`, then find `(ar triangle ABC)/(ar triangle PQR)`
ABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such that PQ || BC and divides triangle ABC into two parts equal in area. Find the value of ratio BP : AB.
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3 : 5,

Find:
- ∆APB : ∆CPB
- ∆DPC : ∆APB
- ∆ADP : ∆APB
- ∆APB : ∆ADB
In the following figure, point D divides AB in the ratio 3 : 5. Find :
BC = 4.8 cm, find the length of DE.

A map is drawn to scale of 1:20000. Find: The distance covered by 6cm on the map
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that b2 + c2 = `2"p"^2 + "a"^2/2`
ΔABC ~ ΔDEF. Write the ratios of their corresponding sides
In a square of side 10 cm, its diagonal = ______.
