Advertisements
Advertisements
प्रश्न
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that b2 + c2 = `2"p"^2 + "a"^2/2`
उत्तर
Given ∠AED = 90°
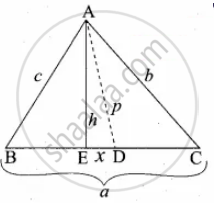
ED = x, DC = `"a"/2` ...(D is the mid point of BC)
∴ EC = `x + "a"/2`, BE = `"a"/2 - x`
∴ In the right ∆AED
AD2 = AE2 + ED2
p2 = h2 + x2
In the right ∆AEC,
AC2 = AE2 + EC2
b2 = `"h"^2 + (x + "a"/2)^2`
= `"h"^2 + x^2 + "a"^2/4 + 2 xx x xx "a"/2`
b2 = `"p"^2 + "a"^2/4 + "a"x` ......(1)
b2 = `"p"^2 + "a"x + 1/4 "a"^2` ....(2)
In the right triangle ABE,
AB2 = AE2 + BE2
c2 = h2 + (a2 – x)2
c2 = h2 + a24 + x2 – ax
c2 = h2 + x2 + 14 a2 – ax
c2 = p2 – ax + `a^2/4` .....(3)
By adding (2) and (3)
b2 + c2 = `"p"^2 + "a"x + "a"^2/4 + "p"^2 - "a"x + "a"^2/4`
= `2"p"^2 + (2"a"^2)/4`
= `2"p"^2 + "a"^2/2`
APPEARS IN
संबंधित प्रश्न
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that `("AO")/("BO") = ("CO")/("DO")`
ΔABC ~ ΔDEF and their areas are respectively `100cm^2` and `49cm2`. If the altitude of ΔABC is 5cm, find the corresponding altitude of ΔDEF.
In the given figure, ∠PQR = ∠PST = 90° ,PQ = 5cm and PS = 2cm.
(i) Prove that ΔPQR ~ ΔPST.
(ii) Find Area of ΔPQR : Area of quadrilateral SRQT.

Δ ABC - Δ XYZ. If area of Δ ABC is 9cm2 and area of Δ XYZ is 16cm2 and if BC= 2.1cm, find the length of YZ.
Figure shows Δ PQR in which ST || QR and SR and QT intersect each other at M. If `"PT"/"TR" = 5/3` find `("Ar" (triangle "MTS"))/("Ar" (triangle "MQR"))`

A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in m, of the aeroplane, if length of its model is 16 cm.
ΔXYZ is enlarged to ΔX'Y'Z'. If XY = 12cm, YZ = 8cm and XZ = 14cm and the smallest side of ΔX'Y'Z' is 12cm, find the scale factor and use it to find the length of the other sides of the image ΔX'Y'Z'.
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The length of the truck
Construct a triangle similar to a given triangle LMN with its sides equal to `4/5` of the corresponding sides of the triangle LMN (scale factor `4/5 < 1`)
A man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4 m from the mirror B, he can see the reflection of the top of the tree. How height is the tree?
