Advertisements
Advertisements
प्रश्न
In the given figure, ∠PQR = ∠PST = 90° ,PQ = 5cm and PS = 2cm.
(i) Prove that ΔPQR ~ ΔPST.
(ii) Find Area of ΔPQR : Area of quadrilateral SRQT.

उत्तर
To prove ΔPQR ∼ ΔPST
In ΔPQR and ΔPST
∠PQR = ∠PST = 90°
∠P = ∠P ( common )
∴ ΔPQR ∼ ΔPST {by AA axiom}
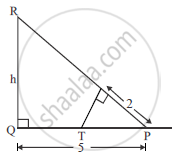
(ii) `("Area of PQR ")/("Area of Quadrilateral")` =
`("ar" (ΔPQR))/("ar" (ΔPST )) = (1/2 xx PQ xx QR )/(1/2 xxPS xx ST) = 5/2 xx 5/2`
`("ar" (ΔPQR))/("ar" (ΔPST )) = 25/4 [ ∵ (PQ)/(PS) = (QR)/(ST) ]`
Taking the reciprocals on both sides
`("ar" (ΔPST ))/("ar" (ΔPQR)) = 4/25`
Now deducting both sides by 1
` therefore 1 - ("ar" (ΔPST ))/("ar" (ΔPQR)) = 1-4/25`
`("ar" (ΔPQR )- "ar" (ΔPST)) /("ar"(ΔPQR)) = 21/25`
`⇒ ("Area of quadrilateral")/("ar"(Delta PQR)) = 21/25`
APPEARS IN
संबंधित प्रश्न
Examine each pair of triangles in Figure, and state which pair of triangles are similar. Also, state the similarity criterion used by you for answering the question and write the similarity relation in symbolic form
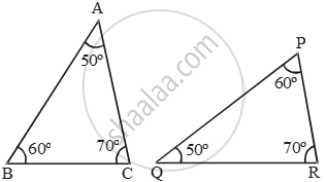
figure (i)
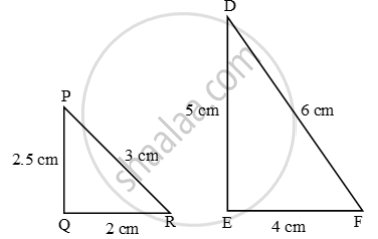
figure 2
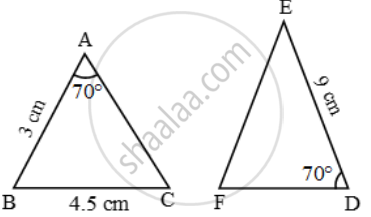
figure 3

figure 4
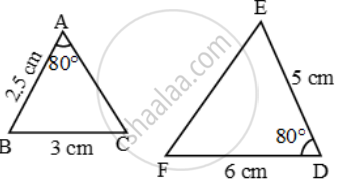
figure 5
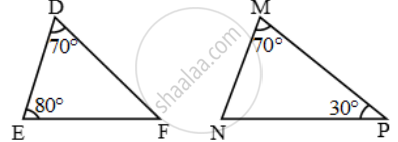
figure 6

figure 7
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

In the given figure, ΔOAB ~ ΔOCD. If AB = 8cm, BO = 6.4cm, OC = 3.5cm and CD = 5cm, find (i) OA (ii) DO.
ABCD is parallelogram and E is a point on BC. If the diagonal BD intersects AE at F, prove that AF × FB = EF × FD.

In a circle, two chords AB and CD intersect at a point P inside the circle. Prove that
(a) ΔPAC ∼PDB (b) PA. PB= PC.PD

State the SSS-similarity criterion for similarity of triangles
In the given figure, X is any point in the interior of triangle. Point X is joined to vertices of triangle. Seg PQ || seg DE, seg QR || seg EF. Fill in the blanks to prove that, seg PR || seg DF.

Proof : In ΔXDE, PQ || DE ...`square`
∴ `"XP"/square = square/"QE"` ...(I) (Basic proportionality theorem)
In ΔXEF, QR || EF ...`square`
∴ `square/square = square/square ..."(II)" square`
∴ `square/square = square/square` ...from (I) and (II)
∴ seg PR || seg DF ...(converse of basic proportionality theorem)
Construct a triangle ABC with side BC = 6 cm, ∠B = 45°, ∠A = 105°. Then construct another triangle whose sides are `(3)/(4)` times the corresponding sides of the ΔABC.
Prove that the external bisector of an angle of a triangle divides the opposite side externally n the ratio of the sides containing the angle.
PR = 26 cm, QR = 24 cm, ∠PAQ = 90°, PA = 6 cm and QA = 8 cm. Find ∠PQR
