Advertisements
Advertisements
प्रश्न
Prove that the external bisector of an angle of a triangle divides the opposite side externally n the ratio of the sides containing the angle.
उत्तर
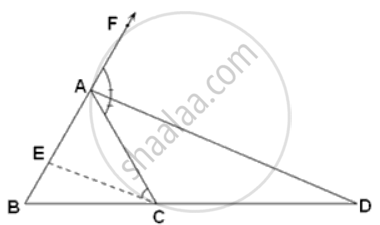
In ΔABC, CE || AD
∴ `"BD"/"CD" = "AB"/"AE"`.....(i)
(By Basic Proportionality theorem)
AD is e bisector of ∠CAF
∠FAD = ∠CAD......(ii)
Since CE || AD
Therefore,
∠ACE = ∠CAD......(iii) ...(alternate angles)
∠AEC = ∠FAD......(iv) ...(corresponding angles)
From (ii) and (iii) and (iv)
∠AEC = ∠ACE
In ΔAEC,
∠AEC = ∠ACE
AC = AE ......(v) ...(Equal angles have equal sides opposite to them)
From (i) and (v)
`"BD"/"CD" = "AB"/"AC"`.
APPEARS IN
संबंधित प्रश्न
State, true or false:
All isosceles triangles are similar.
In the given figure, ∠PQR = ∠PST = 90° ,PQ = 5cm and PS = 2cm.
(i) Prove that ΔPQR ~ ΔPST.
(ii) Find Area of ΔPQR : Area of quadrilateral SRQT.

An aeroplane is 30m long and its model is l5 cm long. If the total outer surface area of the model is 150 cm2 , find the cost of painting the outer surface of the aeroplane at Rs. 120 per m2, if 5O m2 is left out for windows.
The dimensions of the model of a multistorey building are 1.2 m × 75 cm × 2 m. If the scale factor is 1 : 30; find the actual dimensions of the building.
The given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.

In ΔABC, DE is parallel to BC and DE = 3:8.
Find:
(i) AD : BD
(ii) AE, if AC = 16.
ΔABC has been reduced by a scale factor 0.6 to ΔA'B'C'/ Calculate:Length of B' C', if BC = 8cm
If ∆ABC ~ ∆DEF such that area of ∆ABC is 9 cm2 and the area of ∆DEF is 16 cm2 and BC = 2.1 cm. Find the length of EF.
The perimeters of two similar triangles ∆ABC and ∆PQR are 36 cm and 24 cm respectively. If PQ = 10 cm, then the length of AB is
It is given that ΔABC ~ ΔPQR, with `(BC)/(QR) = 1/3`. Then, `(ar(PRQ))/(ar(BCA))` is equal to ______.
