Advertisements
Advertisements
प्रश्न
AM and DN are the altitudes of two similar triangles ABC and DEF. Prove that: AM : DN = AB : DE.
उत्तर
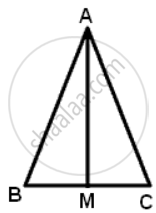
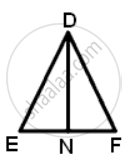
Since ΔABC ∼ ΔDEF
∠B = ∠E
∠AMB = ∠DNE ...(Both are right angles)
Therefore, ΔANB ∼ ΔDNE
∴ `"AM"/"DN" = "AB"/"DE"`
⇒ AM : DN = AB:DE.
APPEARS IN
संबंधित प्रश्न
Prove that the area of Δ BCE described on one side BC of a square ABCD is one half the area of the similar Δ ACF described on the diagonal AC.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : OC', if OC = 21 cm.
Also, state the value of :
- `(OB^')/(OB)`
- `(C^'A^')/(CA)`
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and angle ABC = 90°.
Calculate : the area of the plot in sq. km.
In the following figure, point D divides AB in the ratio 3 : 5. Find :
- `(AE)/(EC)`
- `(AD)/(AB)`
- `(AE)/(AC)`
Also, if: - DE = 2.4 cm, find the length of BC.
- BC = 4.8 cm, find the length of DE.

In the following figure, point D divides AB in the ratio 3 : 5. Find : `(AE)/(AC)`

In the adjoining figure, the medians BD and CE of a ∆ABC meet at G. Prove that
(i) ∆EGD ∼ ∆CGB and
(ii) BG = 2GD for (i) above.
Find the scale factor in each of the following and state the type of size transformation:
Image length = 8cm, Actual length = 20cm.
On a map drawn to a scale of 1: 2,50,000, a triangular plot of land has the following measurements:
AB = 3 cm, BC = 4 cm, ∠ABC = 90°. Calculate:
(i) The actual length of AB in km.
(ii) The area of Plot in sq. km.
A map is drawn to scale of 1:20000. Find: The area of the lake on the map which has an actual area of 12km2
If in triangles PQR and XYZ, `"PQ"/"XY" = "QR"/"ZX"` then they will be similar if
