Advertisements
Advertisements
प्रश्न
Prove that the area of Δ BCE described on one side BC of a square ABCD is one half the area of the similar Δ ACF described on the diagonal AC.
उत्तर
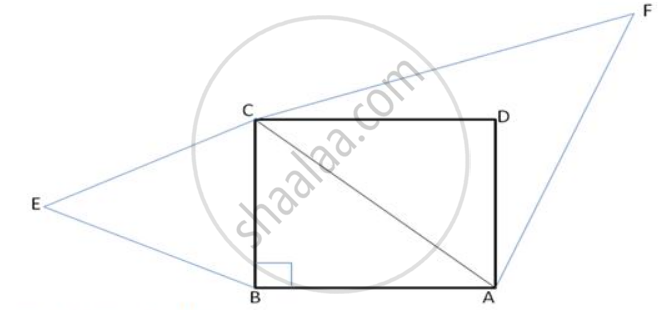
In right angled triangle ABC ,
By Pythagoras Theorem , AB2 + BC2 = AC2
Given , Δ BCE ∼ Δ ACF
`("Ar" triangle "BCE")/("Ar" triangle "ACF") = "BC"^2/"AC"^2`
[The ration of areas of two similar triangle is equal to the ratio of square of their corresponding sides.]
`= "BC"^2/"AC"^2`
`= 1/2`
Required ratio is 1 : 2.
APPEARS IN
संबंधित प्रश्न
Prove that the angle bisector of a triangle divides the side opposite to the angle in the ratio of the remaining sides.
In the following figure, if LM || CB and LN || CD, prove that `("AM")/("AB")=("AN")/("AD")`

In the given figure, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC ∼ ΔPDB
(ii) PA.PB = PC.PD

Prove that, in a right triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides.
The perimeters of two similar triangles are 25 cm and 15 cm respectively. If one side of first triangle is 9 cm, what is the corresponding side of the other triangle?
In triangle ABC, DE is parallel to BC; where D and E are the points on AB and AC respectively.
Prove: ∆ADE ~ ∆ABC.
Also, find the length of DE, if AD = 12 cm, BD = 24 cm BC = 8 cm.
P and Q are points on the sides AB and AC respectively of a ΔABC. If AP = 2cm, PB = 4cm, AQ = 3cm and QC = 6cm, show that BC = 3PQ.
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in m, of the aeroplane, if length of its model is 16 cm.
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆LOP ~ ∆QMO

Are triangles in figure similar? If yes, then write the test of similarity.
