Advertisements
Advertisements
Question
Prove that the area of Δ BCE described on one side BC of a square ABCD is one half the area of the similar Δ ACF described on the diagonal AC.
Solution
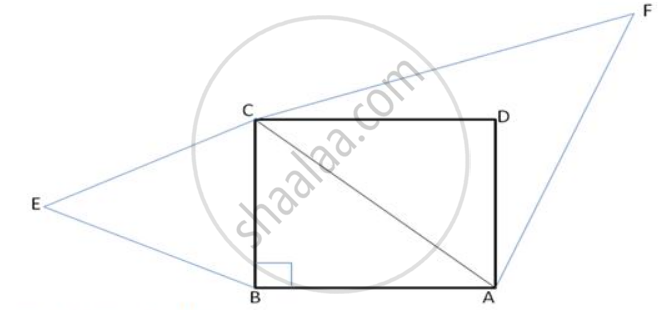
In right angled triangle ABC ,
By Pythagoras Theorem , AB2 + BC2 = AC2
Given , Δ BCE ∼ Δ ACF
`("Ar" triangle "BCE")/("Ar" triangle "ACF") = "BC"^2/"AC"^2`
[The ration of areas of two similar triangle is equal to the ratio of square of their corresponding sides.]
`= "BC"^2/"AC"^2`
`= 1/2`
Required ratio is 1 : 2.
APPEARS IN
RELATED QUESTIONS
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :

- ΔADE ∼ ΔACB.
- If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
- Find, area of ΔADE : area of quadrilateral BCED.
The areas of two similar triangles are 169cm2 and 121cm2 respectively. If the longest side of the larger triangle is 26cm, find the longest side of the smaller triangle.
A triangle LMN has been reduced by scale factor 0.8 to the triangle L' M' N'. Calculate: the length of LM, if L' M' = 5.4 cm.
Choose the correct alternative:
If ΔABC ~ ΔPQR and 4A (ΔABC) = 25 A(ΔPQR), then AB : PQ = ?
In ΔABC, point D divides AB in the ratio 5:7, Find: `"AD"/"AB"`
In the figure, PR || SQ. If PR = 10cm, PT = 5cm, TQ = 6cm and ST = 9cm, calculate RT and SQ.
Find the scale factor in each of the following and state the type of size transformation:
Actual area = 64m2, Model area = 100cm2
A model of a ship is made to a scale of 1:500. Find: The area other deck o the ship, if the area of the deck of its model is m2
In the given figure, UB || AT and CU ≡ CB Prove that ΔCUB ~ ΔCAT and hence ΔCAT is isosceles.
In figure, if AD = 6cm, DB = 9cm, AE = 8cm and EC = 12cm and ∠ADE = 48°. Find ∠ABC.

