Advertisements
Advertisements
प्रश्न
Prove that the area of Δ BCE described on one side BC of a square ABCD is one half the area of the similar Δ ACF described on the diagonal AC.
उत्तर
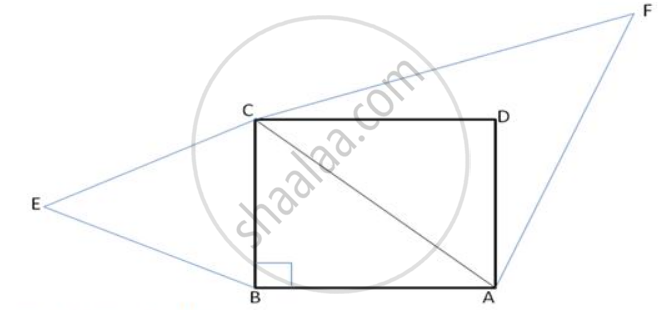
In right angled triangle ABC ,
By Pythagoras Theorem , AB2 + BC2 = AC2
Given , Δ BCE ∼ Δ ACF
`("Ar" triangle "BCE")/("Ar" triangle "ACF") = "BC"^2/"AC"^2`
[The ration of areas of two similar triangle is equal to the ratio of square of their corresponding sides.]
`= "BC"^2/"AC"^2`
`= 1/2`
Required ratio is 1 : 2.
APPEARS IN
संबंधित प्रश्न
Prove that the angle bisector of a triangle divides the side opposite to the angle in the ratio of the remaining sides.
In the adjoining figure, ABC is a right angled triangle with ∠BAC = 90°.
1) Prove ΔADB ~ ΔCDA.
2) If BD = 18 cm CD = 8 cm Find AD.
3) Find the ratio of the area of ΔADB is to an area of ΔCDA.

In the given figure, BC is parallel to DE. Area of triangle ABC = 25 cm2, Area of trapezium BCED = 24 cm2 and DE = 14 cm. Calculate the length of BC. Also, find the area of triangle BCD.

In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:

The perimeter of two similar triangles ABC and PQR are 32cm and 24cm respectively. If PQ = 12cm, find AB.
State the SAS-similarity criterion
Prove that the area of the triangle BCE described on one side BC of a square ABCD as base is one half of the area of similar triangle ACF described on the diagonal AC as base.
If ΔABC, D and E are points on AB and AC. Show that DE || BC for each of the following case or not:
AB = 5.6cm, AD = 1.4cm, AC = 7.2cm, and AE = 1.8cm
In the given figure AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 4 cm, BD = 5 cm and DE = y cm. Find x and y.
In given fig., quadrilateral PQRS, side PQ || side SR, AR = 5 AP, then prove that, SR = 5PQ
