Advertisements
Advertisements
प्रश्न
If Δ ABC , MN || BC .
If AN : AC= 5 : 8, find ar(Δ AMN) : ar(Δ ABC)
उत्तर
Given : `"AN"/"AC" = 5/8`
To Find : `("Ar" triangle "AMN")/("Ar" triangle "ABC")`
In Δ AMN and Δ ABC
∠AMN = ∠ ACB ....(corresponding angles)
∠ ABC = ∠ ACB
∴ Δ AMN ∼ Δ ABC .....(AA corollary)
∴ `("Ar" triangle "AMN")/("Ar" triangle "ABC") = "AN"^2/"AC"^2`
[The ration of areas of two similar triangle is equal to the ratio of square of their corresponding sides.]
`= (5/8)^2`
`("Ar" triangle "AMN")/("Ar" triangle "ABC") = 25/64`
Required ratio is 25 : 64.
APPEARS IN
संबंधित प्रश्न
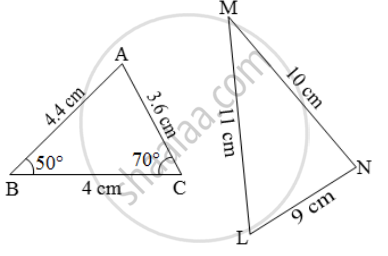
In figure, find ∠L
E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR.
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
In the following figure, if LM || CB and LN || CD, prove that `("AM")/("AB")=("AN")/("AD")`
State, true or false:
Two similar polygons are necessarily congruent.
The given figure shows a triangle PQR in which XY is parallel to QR. If PX : XQ = 1 : 3 and QR = 9 cm, find the length of XY.
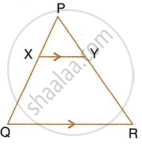
Further, if the area of ΔPXY = x cm2; find, in terms of x the area of :
- triangle PQR.
- trapezium XQRY.
ΔABC~ΔPQR and ar(ΔABC) = 4, ar(ΔPQR) . If BC = 12cm, find QR.
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in m, of the aeroplane, if length of its model is 16 cm.
In ΔABC, D and E are the points on sides AB and AC respectively. Find whether DE || BC, if AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
A plot of land of area 20km2 is represented on the map with a scale factor of 1:200000. Find: The area on the map that represented the plot of land.
In ΔABC, AP ⊥ BC and BQ ⊥ AC, B−P−C, A−Q−C, then show that ΔCPA ~ ΔCQB. If AP = 7, BQ = 8, BC = 12, then AC = ?
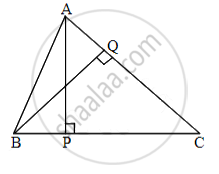
In ΔCPA and ΔCQB
∠CPA ≅ [∠ ______] ...[each 90°]
∠ACP ≅ [∠ ______] ...[common angle]
ΔCPA ~ ΔCQB ......[______ similarity test]
`"AP"/"BQ" = (["______"])/"BC"` .......[corresponding sides of similar triangles]
`7/8 = (["______"])/12`
AC × [______] = 7 × 12
AC = 10.5
