Question

In the adjoining figure, ABC is a right angled triangle with ∠BAC = 90°.

1) Prove ΔADB ~ ΔCDA.

2) If BD = 18 cm CD = 8 cm Find AD.

3) Find the ratio of the area of ΔADB is to an area of ΔCDA.

Answer 1

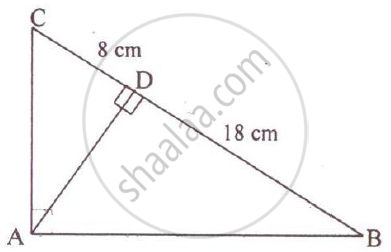
1) Let ∠CAD = x

⇒ ∠DAB = 90° - x

∠DAB = 180 - (90° + 90° - x) = x

∠CAD =- ∠DBA .....(1)

In ΔADB and ΔCDA

∠ADB = ∠ADC     [each 90°]

∠ABD = ∠CAD     [From 1]

∴ ΔADB ~ ΔCDA     (AA similarity criterion)

2) Since the corresponding sides of similar triangles are proportional.

`:. (CD)/(AD) = (DA)/(DB)`

`=> AD^2 = DB xx CD`

`=> AD^2 = 18 xx 8`

`=> AD = 12 cm`

3) The ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.

So `(Ar(ΔADB))/(Ar(ΔCDA)) = ("AD"^2)/"CD"^2 = 144/64 = 9/4`

Thus, the required ratio is 9: 4.