Advertisements
Advertisements
प्रश्न
ABCD is a parallelogram. Point P divides AB in the ratio 2:3 and point Q divides DC in the ratio 4:1. Prove that OC is half of OA.

उत्तर
ABCD is a parallelogram.
AB = DC = a
Point P divides AB in the ratio 2:3
AP = `2/5a`, BP = `3/5a`
Point Q divides DC in the ratio 4:1.
DQ = `4/5a`, CQ = `1/5a`
ΔAPO ∼ ΔCQO ...[AA similarity]
`(AP)/(CQ) = (PO)/(QO) = (AO)/(CO)`
`(AO)/(CO) = (2/5a)/(1/5a) = 2/1`
`\implies` OC = `1/2 OA`
APPEARS IN
संबंधित प्रश्न
Prove that the angle bisector of a triangle divides the side opposite to the angle in the ratio of the remaining sides.
In figure, ∠CAB = 90º and AD ⊥ BC. If AC = 75 cm, AB = 1 m and BD = 1.25 m, find AD.
In figure, considering triangles BEP and CPD, prove that BP × PD = EP × PC.
In figure, ∠A = ∠CED, prove that ∆CAB ~ ∆CED. Also, find the value of x.

A vertical stick 20 cm long casts a shadow 6 cm long on the ground. At the same time, a tower casts a shadow 15 m long on the ground. Find the height of the tower.
The ratio between the corresponding sides of two similar triangles is 2 is to 5. Find the ratio between the areas of these triangles.
The given figure shows a triangle PQR in which XY is parallel to QR. If PX : XQ = 1 : 3 and QR = 9 cm, find the length of XY.

Further, if the area of ΔPXY = x cm2; find, in terms of x the area of :
- triangle PQR.
- trapezium XQRY.
In each of the given pairs of triangles, find which pair of triangles are similar. State the similarity criterion and write the similarity relation in symbolic form:
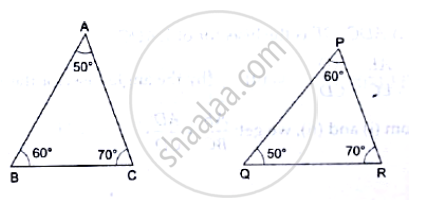
State the SAS-similarity criterion
∆ABC and ∆DEF are equilateral triangles, A(∆ABC): A(∆DEF) = 1: 2. If AB = 4 then what is length of DE?

In the figure, parts of the two triangles bearing identical marks are
congruent. State the test by which the triangles are congruent.

In figure , DEF is a right -angled triangle with ∠ E = 90 °.FE is produced to G and GH is drawn perpendicular to DE = 8 cm , DH = 8 cm ,DH = 6 cm and HF = 4 cm , find `("Ar" triangle "DEF")/("Ar" triangle "GHF")`

A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : OA, if OA' = 6 cm.
The model of a building is constructed with scale factor 1:30.
(i) If the height of the model is 80 cm, find the actual height of the building in metres.
(ii) If the actual volume of a tank at the top of the building is 27 m3, find the volume of the tank on the top of the model.
D and E are points on the sides AB and AC respectively of a Δ ABC such that DE | | BC and divides Δ ABC into two parts, equal in area. Find `"BD"/"AB"`.
If ΔABC, D and E are points on AB and AC. Show that DE || BC for each of the following case or not:
AB = 5.6cm, AD = 1.4cm, AC = 7.2cm, and AE = 1.8cm
If ΔABC, D and E are points on AB and AC. Show that DE || BC for each of the following case or not:
AD = 5.7cm, BD = 9.5cm, AE = 3.3cm, and EC = 5.5cm
In figure, PQ is parallel to BC, AP : AB = 2 : 7. If QC = 0 and BC = 21,
Find
(i) AQ
(ii) PQ
In ΔABC, BP and CQ are altitudes from B and C on AC and AB respectively. BP and CQ intersect at O. Prove that
(i) PC x OQ = QB x OP
(ii) `"OC"^2/"OB"^2 = ("PC" xx "PO")/("QB" xx "QO")`
Prove that the external bisector of an angle of a triangle divides the opposite side externally n the ratio of the sides containing the angle.
Two figures are similar. If the ratio of their perimeters is 8:16. What will be the ratio of the corresponding sides?
The areas of two similar triangles are 169cm2 and 121cm2 respectively. If one side of the larger triangle is 26cm, find the length of the corresponding side of the smaller triangle.
In ΔABC, AB = 8cm, AC = 10cm and ∠B = 90°. P and Q are the points on the sides AB and AC respectively such that PQ = 3cm ad ∠PQA = 90. Find: The area of ΔAQP.
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The volume of the model if the volume of the truck is 6m3
Two triangles QPR and QSR, right angled at P and S respectively are drawn on the same base QR and on the same side of QR. If PR and SQ intersect at T, prove that PT × TR = ST × TQ
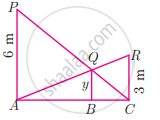
Two vertical poles of heights 6 m and 3 m are erected above a horizontal ground AC. Find the value of y
If ∆ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is
In the given figure, UB || AT and CU ≡ CB Prove that ΔCUB ~ ΔCAT and hence ΔCAT is isosceles.
If in triangles PQR and XYZ, `"PQ"/"XY" = "QR"/"ZX"` then they will be similar if
ΔABC ~ ΔPQR, A(ΔABC) = 80 sq.cm, A(ΔPQR) = 125 sq.cm, then complete `("A"(Δ"ABC"))/("A"(Δ"PQR")) = 80/125 = (["______"])/(["______"])`, hence `"AB"/"PQ" = (["______"])/(["______"])`
