Advertisements
Advertisements
प्रश्न
The areas of two similar triangles are 169cm2 and 121cm2 respectively. If one side of the larger triangle is 26cm, find the length of the corresponding side of the smaller triangle.
उत्तर
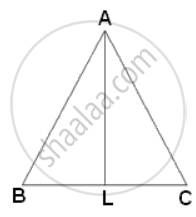
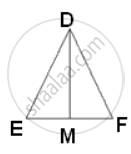
The ratio of the areas of two similar triangles is equal to the ratio of the squares of the corresponding sides.
∴ `("area"(Δ"ABC"))/("area"(Δ"PQR")) = "AB"^2/"DE"^2`
⇒ `(169)/(121) = (26^2)/"DE"^2`
⇒ DE2 = `(121 xx 676)/(169)`
⇒ DE2 = 484
⇒ DE = 22cm.
APPEARS IN
संबंधित प्रश्न
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC in L and AD produced in E. Prove that EL = 2 BL
In ∆ABC, DE is parallel to base BC, with D on AB and E on AC. If `\frac{AD}{DB}=\frac{2}{3}` , find `\frac{BC}{DE}.`
If Δ ABC , MN || BC .

If AN : AC= 5 : 8, find ar(Δ AMN) : ar(Δ ABC)
A model of a ship is made with a scale factor of 1 : 500. Find
The length of the ship, if the model length is 60 cm.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : OA, if OA' = 6 cm.
In ΔABC, point D divides AB in the ratio 5:7, Find: `"AE"/"EC"`
ΔABC is right angled at A. AD is drawn perpendicular to BC. If AB = 8cm and AC = 6cm, calculate BD.
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The length of the truck
In the given figure YH || TE. Prove that ΔWHY ~ ΔWET and also find HE and TE
In the given figure, if ABCD is a trapezium in which AB || CD || EF, then prove that `(AE)/(ED) = (BF)/(FC)`.

