Advertisements
Advertisements
Question
The areas of two similar triangles are 169cm2 and 121cm2 respectively. If one side of the larger triangle is 26cm, find the length of the corresponding side of the smaller triangle.
Solution
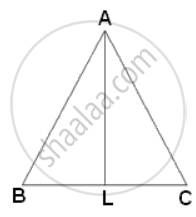
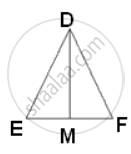
The ratio of the areas of two similar triangles is equal to the ratio of the squares of the corresponding sides.
∴ `("area"(Δ"ABC"))/("area"(Δ"PQR")) = "AB"^2/"DE"^2`
⇒ `(169)/(121) = (26^2)/"DE"^2`
⇒ DE2 = `(121 xx 676)/(169)`
⇒ DE2 = 484
⇒ DE = 22cm.
APPEARS IN
RELATED QUESTIONS
P and Q are points on sides AB and AC respectively of ∆ABC. If AP = 3 cm, PB = 6cm. AQ = 5 cm and QC = 10 cm, show that BC = 3PQ.
In ∆ABC, AP ⊥ BC, BQ ⊥ AC B– P–C, A–Q – C then prove that, ∆CPA ~ ∆CQB. If AP = 7, BQ = 8, BC = 12 then Find AC.

In Δ ABC , DE is parallel to BC and `"AD"/"DB" = 2/7` IF AC = 5 .6 , find AE.
In Δ ABC, D and E are points on the sides AB and AC respectively. If AD= 4cm, DB=4.Scm, AE=6.4cm and EC=7.2cm, find if DE is parallel to BC or not.
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The area in km2 that can be represented by 1 cm2
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in m, of the aeroplane, if length of its model is 16 cm.
In ΔABC, D and E are the points on sides AB and AC respectively. Find whether DE || BC, if AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
On a map drawn to a scale of 1:25000, a triangular plot of land is right angled and the sides forming the right angle measure 225cm and 64cm.Find: The area of the plot in sq. km.
If BD ⊥ AC and CE ⊥ AB, prove that `"CA"/"AB" = "CE"/"DB"`

Areas of two similar triangles are 225 cm2 and 81 cm2. If side of smaller triangle is 12 cm, find corresponding side of major triangle.
