Advertisements
Advertisements
Question
In ΔABC, D and E are the points on sides AB and AC respectively. Find whether DE || BC, if AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
Solution
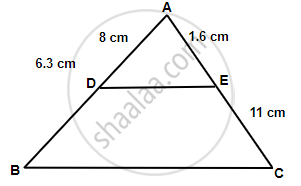
In ΔADE and ΔABC,
`(AE)/(EC) = 1.6/11 = 0.8/5.5`
`(AD)/(BD) = (0.8)/(6.3 - 8) = 0.8/5.5`
So, `(AE)/(EC) = (AD)/(BD)`
∴ DE || BC ...(By the converse of mid-point theorem)
APPEARS IN
RELATED QUESTIONS
See the given figure. DE || BC. Find AD.

Using Basic proportionality theorem, prove that a line drawn through the mid-points of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : OC', if OC = 21 cm.
Also, state the value of :
- `(OB^')/(OB)`
- `(C^'A^')/(CA)`
A model of an aeroplane is made to a scale of 1 : 400. Calculate : the length, in cm, of the model; if the length of the aeroplane is 40 m.
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and ∠ABC = 90°.
Calculate : the actual lengths of AB and BC in km.
In the following figure, point D divides AB in the ratio 3 : 5. Find :
DE = 2.4 cm, find the length of BC.

In the given figure, ΔABC ~ ΔADE. If AE : EC = 4 : 7 and DE = 6.6 cm, find BC. If 'x' be the length of the perpendicular from A to DE, find the length of perpendicular from A to BC in terms of 'x'.

In ΔABC, point D divides AB in the ratio 5:7, Find: BC, If DE = 2.5cm
ΔABC ~ ΔDEF. Write the ratios of their corresponding sides
In the adjoining diagram the length of PR is ______.

