Advertisements
Advertisements
Question
In ΔABC, D and E are the points on sides AB and AC respectively. Find whether DE || BC, if:
- AB = 9 cm, AD = 4 cm, AE = 6 cm and EC = 7.5 cm.
- AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
Solution
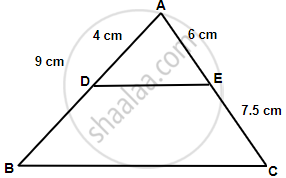
i. In ΔADE and ΔABC,
`(AE)/(EC) = 6/7.5 = 4/5`
`(AD)/(BD) = 4/5` ...(Since AB = 9 cm and AD = 4 cm)
So, `(AE)/(EC) = (AD)/(BD)`
∴ DE || BC ...(By the converse of mid-point theorem)
ii. In ΔADE and ΔABC,
`(AE)/(EC) = 1.6/11 = 0.8/5.5`
`(AD)/(BD) = (0.8)/(6.3 - 8) = 0.8/5.5`
So, `(AE)/(EC) = (AD)/(BD)`
∴ DE || BC ...(By the converse of mid-point theorem)
APPEARS IN
RELATED QUESTIONS
In figure, considering triangles BEP and CPD, prove that BP × PD = EP × PC.
The diagonals of a quadrilateral ABCD intersect each other at the point O such that `("AO")/("BO") = ("CO")/("DO")`. Show that ABCD is a trapezium.
In the given figure, QR is parallel to AB and DR is parallel to AB and DR is parallel to QB.

Prove that: PQ2 = PD × PA.
In the figure, given below, the medians BD and CE of a triangle ABC meet at G. Prove that:

- ΔEGD ~ ΔCGB and
- BG = 2GD from (i) above.
In ΔABC, D and E are the points on sides AB and AC respectively. Find whether DE || BC, if AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
ΔABC is right angled at A. AD is drawn perpendicular to BC. If AB = 8cm and AC = 6cm, calculate BD.
The areas of two similar triangles are 16cm2 and 9cm2 respectively. If the altitude of the smaller triangle is 1.8cm, find the length of the altitude corresponding to the larger triangle.
From the given figure, prove that ΔABC ~ ΔEDF
∆ABC ~ ∆PQR. If AM and PN are altitudes of ΔABC and ∆PQR respectively and AB2 : PQ2 = 4 : 9, then AM : PN = ______.

In ΔABC, DE || BC (as shown in the figure), If AD = 4 cm, AB = 9 cm and AC = 13.5 cm, then the length of EC is ______.
