Advertisements
Advertisements
प्रश्न
In ΔABC, D and E are the points on sides AB and AC respectively. Find whether DE || BC, if:
- AB = 9 cm, AD = 4 cm, AE = 6 cm and EC = 7.5 cm.
- AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
उत्तर
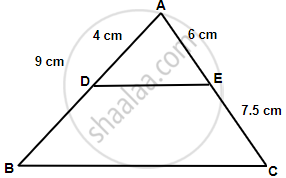
i. In ΔADE and ΔABC,
`(AE)/(EC) = 6/7.5 = 4/5`
`(AD)/(BD) = 4/5` ...(Since AB = 9 cm and AD = 4 cm)
So, `(AE)/(EC) = (AD)/(BD)`
∴ DE || BC ...(By the converse of mid-point theorem)
ii. In ΔADE and ΔABC,
`(AE)/(EC) = 1.6/11 = 0.8/5.5`
`(AD)/(BD) = (0.8)/(6.3 - 8) = 0.8/5.5`
So, `(AE)/(EC) = (AD)/(BD)`
∴ DE || BC ...(By the converse of mid-point theorem)
APPEARS IN
संबंधित प्रश्न
The ratio between the corresponding sides of two similar triangles is 2 is to 5. Find the ratio between the areas of these triangles.
Area of two similar triangles are 98 sq. cm and 128 sq. cm. Find the ratio between the lengths of their corresponding sides.
In the given figure, A – D – C and B – E – C seg DE || side AB If AD = 5, DC = 3, BC = 6.4 then Find BE.

In the adjoining figure. BC is parallel to DE, area of ΔABC = 25 sq cm, area of trapezium BCED = 24 sq cm, DE = 14 cm. Calculate the length of BC.
ΔABC is right angled at A. AD is drawn perpendicular to BC. If AB = 8cm and AC = 6cm, calculate BD.
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The area of the plot in sq km
ΔPQR ~ ΔSUV. Write pairs of congruent angles
ΔABP ~ ΔDEF and A(ΔABP) : A(ΔDEF) = 144:81, then AB : DE = ?
In triangle ABC point D is on side BC (B−D−C) such that ∠BAC = ∠ADC then prove that CA2 = CB × CD
In the figure PQ || BC. If `"PQ"/"BC" = 2/5` then `"AP"/"PB"` is ______.

