Advertisements
Advertisements
प्रश्न
In the given figure, A – D – C and B – E – C seg DE || side AB If AD = 5, DC = 3, BC = 6.4 then Find BE.

उत्तर
Let BE be x.
BE + CE = BC ...(∵ B - E - C)
∴ x + CE = 6.4
∴ CE = (6.4 − x)
In Δ ABC,
seg DE || side AB ...(Given)
∴ By basic proportionality theorem,
`("CD")/("DA") = ("CE")/("BE")`
∴ `3/5 = (6.4 - "x")/"x"`
∴ 3x = 5(6.4 − x)
∴ 3x = 32 − 5x
∴ 3x + 5x = 32
∴ 8x = 32
∴ x = `32/8`
∴ x = 4
BE = x = 4
∴ BE = 4
APPEARS IN
संबंधित प्रश्न
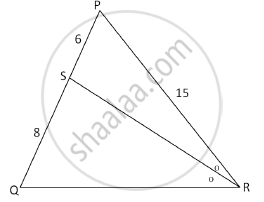
In the following figure, in ΔPQR, seg RS is the bisector of ∠PRQ. If PS = 6, SQ = 8, PR = 15, find QR.
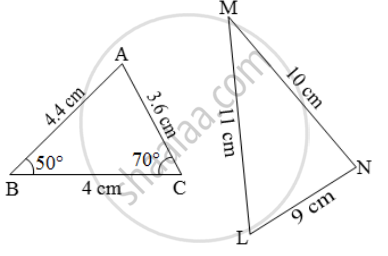
In figure, find ∠L
A vertical stick 20 cm long casts a shadow 6 cm long on the ground. At the same time, a tower casts a shadow 15 m long on the ground. Find the height of the tower.
Given: ∠GHE = ∠DFE = 90°,
DH = 8, DF = 12,
DG = 3x – 1 and DE = 4x + 2.
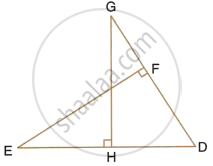
Find: the lengths of segments DG and DE.
In the given figure, ΔOAB ~ ΔOCD. If AB = 8cm, BO = 6.4cm, OC = 3.5cm and CD = 5cm, find (i) OA (ii) DO.
In the figure , ABCD is a quadrilateral . F is a point on AD such that AF = 2.1 cm and FD = 4.9 cm . E and G are points on AC and AB respectively such that EF || CD and GE || BC . Find `("Ar" triangle "BCD")/("Ar" triangle "GEF")`
Δ ABC ∼ Δ PQR such that AB= 1.5 cm and PQ=2. 1 cm. Find the ratio of areas of Δ ABC and ΔPQR.
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The number of kilometres on the ground represented by lcm or the map
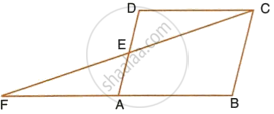
The given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.
Let ∆ ABC ∽ ∆ DEF and their areas be respectively, 64 cm2 and 121 cm2. If EF = 15⋅4 cm, find BC.
Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
In figure, PQ is parallel to BC, AP : AB = 2 : 7. If QC = 0 and BC = 21,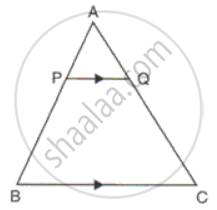
Find
(i) AQ
(ii) PQ
In ΔABC, MN is drawn parallel to BC. If AB = 3.5cm, AM : AB = 5 : 7 and NC = 2cm, find:
(i) AM
(ii) AC
AM and DN are the altitudes of two similar triangles ABC and DEF. Prove that: AM : DN = AB : DE.
In ΔABC, AB = 8cm, AC = 10cm and ∠B = 90°. P and Q are the points on the sides AB and AC respectively such that PQ = 3cm ad ∠PQA = 90. Find: Area of quadrilateral PBCQ: area of ΔABC.
The scale of a map is 1 : 50000. The area of a city is 40 sq km which is to be represented on the map. Find: The area of land represented on the map.
A map is drawn to scale of 1:20000. Find: The distance on the map representing 4km
A model of a ship is made to a scale of 1:500. Find: The volume of the model when the volume of the ship is 1km3
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that c2 = `"p"^2 - "a"x + "a"^2/4`
If in triangles PQR and XYZ, `"PQ"/"XY" = "QR"/"ZX"` then they will be similar if
