Advertisements
Advertisements
प्रश्न
In ΔABC, AB = 8cm, AC = 10cm and ∠B = 90°. P and Q are the points on the sides AB and AC respectively such that PQ = 3cm ad ∠PQA = 90. Find: Area of quadrilateral PBCQ: area of ΔABC.
उत्तर
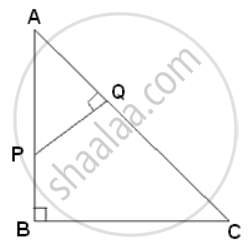
In ΔAQP and ΔABC
∠A = ∠A
∠PQA = ∠ABC ...(right angles)
Therefore, ΔAQP ∼ ΔABC
Area(trapezium EDBC) = Area(ΔABC) - Area(ΔAQP)
Area(trapezium EDBC) = 24 - 6 = 18cm2
`("Area"("trapeziumEDBC"))/("Area"(Δ"ABC")) = (18)/(24)`
⇒ `("Area"("trapeziumEDBC"))/("Area"(Δ"ABC")) = (3)/(4)`
Area(trapezium EDBC): Area(ΔABC) = 3:4.
APPEARS IN
संबंधित प्रश्न
If a perpendicular is drawn from the vertex containing the right angle of a right triangle to the hypotenuse then prove that the triangle on each side of the perpendicular are similar to each other and to the original triangle. Also, prove that the square of the perpendicular is equal to the product of the lengths of the two parts of the hypotenuse
In ∆ABC, DE is parallel to base BC, with D on AB and E on AC. If `\frac{AD}{DB}=\frac{2}{3}` , find `\frac{BC}{DE}.`
E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR.
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
In the given figure, AB and DE are perpendicular to BC.

1) Prove that ΔABC ∼ ΔDEC
2) If AB = 6 cm; DE = 4 cm and AC = 15 cm. Calculate CD.
3) Find the ratio of area of ΔABC: area of ΔDEC
In the given triangle P, Q and R are the mid-points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.

In Δ PQR, MN is drawn parallel to QR. If PM = x, MQ = (x-2), PN = (x+2) and NR = (x-1), find the value of x.
In the following figure, point D divides AB in the ratio 3 : 5. Find : `(AD)/(AB)`

On a map drawn to scale of 1 : 2,50,000 a rectangular plot of land ABCD has the following measurement AB = 12 cm, BC = 16 cm angles A, B, C, and D are 900 each. Calculate:
(i) The diagonal distance of the plot of land in
(ii) Actual length of diagonal.
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that b2 = `"p"^2 + "a"x + "a"^2/4`
In any triangle _______ sides are opposite to equal angles
