Question

In ΔABC, AB = 8cm, AC = 10cm and ∠B = 90°. P and Q are the points on the sides AB and AC respectively such that PQ = 3cm ad ∠PQA = 90. Find: The area of ΔAQP.

Answer 1

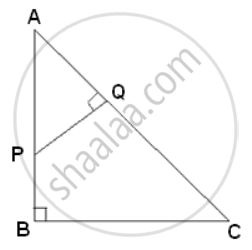
In ΔAQP and ΔABC
∠A = ∠A
∠PQA = ∠ABC    ...(right angles)
Therefore, ΔAQP ∼ ΔABC
By Pythagoras theorem,
BC² = AC² - AB²
⇒ BC² = 10² - 8²
⇒ BC² = 100 - 64
⇒ BC² = 36
⇒ BC = 6cm

Area (ΔABC) `(1)/(2) xx "AB" xx "BC"`

Area (ΔABC) `(1)/(2) xx 8 xx 6`

Area (ΔABC) = 24cm2
Since ΔAQP ∼ ΔABC

`("Area"(Δ"AQP"))/("Area"(Δ"ABC")) = "PQ"^2/"BC"^2`

`("Area"(Δ"AQP"))/("Area"(Δ"ABC")) = 3^2/6^2`

⇒ Area(ΔAQP) = `(9 xx 24)/(36)`

⇒ Area(ΔAQP) = 6cm² .