Advertisements
Advertisements
प्रश्न
In ΔABC, DE is drawn parallel to BC cutting AB in the ratio 2 : 3. Calculate:
(i) `("area"(Δ"ADE"))/("area"(Δ"ABC")`
(i) `("area"("trapeziumEDBC"))/("area"(Δ"ABC"))`
उत्तर
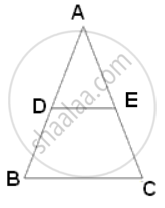
AD : DB = 2 : 3
AB
= AD + DB
= 2 + 3
= 5
(i) `("area"(Δ"ADE"))/("area"(Δ"ABC")) = "AD"^2/"AB"^2`
⇒ `("area"(Δ"ADE"))/("area"(Δ"ABC")) = (2^2)/(5^2)`
⇒ `("area"(Δ"ADE"))/("area"(Δ"ABC")) = (4)/(25)`.
(ii) `("area"("trapeziumEDBC"))/("area"(Δ"ABC")) = ("area"(Δ"ABC") - "area"(Δ"ADE"))/("area"(Δ"ABC"))`
⇒ `("area"("trapeziumEDBC"))/("area"(Δ"ABC")) = (25 - 4)/(25)`
⇒ `("area"("trapeziumEDBC"))/("area"(Δ"ABC")) = (21)/(25)`.
APPEARS IN
संबंधित प्रश्न
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC in L and AD produced in E. Prove that EL = 2 BL
In the following figure, DE || OQ and DF || OR, show that EF || QR.

ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :

- ΔADE ∼ ΔACB.
- If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
- Find, area of ΔADE : area of quadrilateral BCED.
Area of two similar triangles are 98 sq. cm and 128 sq. cm. Find the ratio between the lengths of their corresponding sides.
In Δ ABC, DE || BC; DC and EB intersects at F. if `"DE"/"BC" = 2/7` , find `("Ar" (triangle "FDE"))/("Ar" (triangle "FBC"))`
Δ ABC is similar to Δ PQR. If AB = 6cm, BC = 9cm, PQ = 9cm and PR = 10.5cm, find the lengths of AC and QR.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : BC, if B' C' = 15 cm.
In ΔABC, point D divides AB in the ratio 5:7, Find: BC, If DE = 2.5cm
The areas of two similar triangles are 169cm2 and 121cm2 respectively. If one side of the larger triangle is 26cm, find the length of the corresponding side of the smaller triangle.
Two similar triangles will always have ________ angles
