Advertisements
Advertisements
Question
In ΔABC, DE is drawn parallel to BC cutting AB in the ratio 2 : 3. Calculate:
(i) `("area"(Δ"ADE"))/("area"(Δ"ABC")`
(i) `("area"("trapeziumEDBC"))/("area"(Δ"ABC"))`
Solution
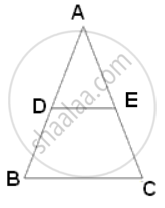
AD : DB = 2 : 3
AB
= AD + DB
= 2 + 3
= 5
(i) `("area"(Δ"ADE"))/("area"(Δ"ABC")) = "AD"^2/"AB"^2`
⇒ `("area"(Δ"ADE"))/("area"(Δ"ABC")) = (2^2)/(5^2)`
⇒ `("area"(Δ"ADE"))/("area"(Δ"ABC")) = (4)/(25)`.
(ii) `("area"("trapeziumEDBC"))/("area"(Δ"ABC")) = ("area"(Δ"ABC") - "area"(Δ"ADE"))/("area"(Δ"ABC"))`
⇒ `("area"("trapeziumEDBC"))/("area"(Δ"ABC")) = (25 - 4)/(25)`
⇒ `("area"("trapeziumEDBC"))/("area"(Δ"ABC")) = (21)/(25)`.
APPEARS IN
RELATED QUESTIONS
In figure, if ∠A = ∠C, then prove that ∆AOB ~ ∆COD

In the given figure, ∠1 = ∠2 and `(AC)/(BD)=(CB)/(CE)` Prove that Δ ACB ~ Δ DCE.
In the following figure, point D divides AB in the ratio 3 : 5. Find :
BC = 4.8 cm, find the length of DE.

In the figure, DE || AC and DC || AP. Prove that `"BE"/"EC" = "BC"/"CP"`
In a quadrilateral PQRS, the diagonals PR and QS intersect each other at the point T. If PT:TR = QT :TS = 1:2, show that TP:TQ = TR:TS
The areas of two similar triangles are 169cm2 and 121cm2 respectively. If one side of the larger triangle is 26cm, find the length of the corresponding side of the smaller triangle.
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that c2 = `"p"^2 - "a"x + "a"^2/4`
Side of equilateral triangle PQR is 8 cm then find the area of triangle whose side is half of the side of triangle PQR.
Is the following statement true? Why? “Two quadrilaterals are similar, if their corresponding angles are equal”.
ABCD is a parallelogram. Point P divides AB in the ratio 2:3 and point Q divides DC in the ratio 4:1. Prove that OC is half of OA.

