Advertisements
Advertisements
Question
D and E are points on the sides AB and AC of ΔABC such that DE | | BC and divides ΔABC into two parts, equal in area. Find `"BD"/"AB"`.
Solution
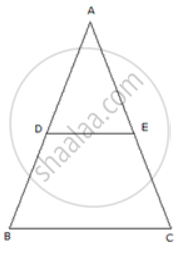
Area(ΔADE) = area(trapezium BCED)
⇒ Area(ΔADE) + Area(ΔADE)
= Area(trapezium BCED) + Area(ΔADE)
⇒ 2 Area(ΔADE) = Area(ΔABC)
In ΔADE and ΔABC,
∠ADE = ∠B ...(corresponding angles)
∠A = ∠A
Therefore, ΔADE ∼ ΔABC
∴ `"area(Δ ADE)"/"area(Δ ABC)" = "AD"^2/"AB"^2`
⇒ `"area(ΔADE)"/(2" x area(ΔADE)") = "AD"^2/"AB"^2`
⇒ `(1)/(2) = ("AD"/"AB")^2`
⇒ `"AD"/"AB" = (1)/sqrt(2)`
⇒ AB = `sqrt(2)"AD"`
⇒ AB = `sqrt(2)("AB - BD")`
⇒ `(sqrt(2) - 1)"AB" = sqrt(2)"BD"`
⇒ `"BD"/"AB" = (sqrt(2) - 1)/(sqrt(2)`
= `(2 - sqrt(2))/(2)`.
APPEARS IN
RELATED QUESTIONS
In the given figure, ΔODC~ΔOBA, ∠BOC = 115° and ∠CDO = 700.
Find (i) ∠DCO (ii) ∠DCO (iii) ∠OAB (iv) ∠OBA.

In the given figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and the distance between AB and AC is 14 cm. If arcs of equal radii 7 cm taking A, B, C and D as centres, have been drawn, then find the area of the shaded region ?

In the figure, parts of the two triangles bearing identical marks are
congruent. State the test by which the triangles are congruent.

A triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A' B' C'. Calculate : the length of C' A' if CA = 4 cm.
In the figure, PQR is a straight line and PS || RT. If QS = 12cm, QR = 15cm, QT = 10cm and RT = 6cm, find PQ and PS.
Find the scale factor in each of the following and state the type of size transformation:
Model volume = 200cm3, Actual volume = 8cm3
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The volume of the model if the volume of the truck is 6m3
If ∆ABC – ∆PQR in which ∠A = 53° and ∠Q = 77°, then ∠R is
ΔABP ~ ΔDEF and A(ΔABP) : A(ΔDEF) = 144:81, then AB : DE = ?
In figure, if AD = 6 cm, DB = 9 cm, AE = 8 cm and EC = 12 cm and ∠ADE = 48°. Find ∠ABC.

