Advertisements
Advertisements
प्रश्न
D and E are points on the sides AB and AC of ΔABC such that DE | | BC and divides ΔABC into two parts, equal in area. Find `"BD"/"AB"`.
उत्तर
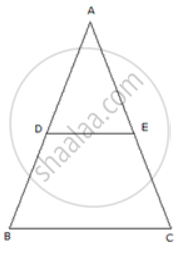
Area(ΔADE) = area(trapezium BCED)
⇒ Area(ΔADE) + Area(ΔADE)
= Area(trapezium BCED) + Area(ΔADE)
⇒ 2 Area(ΔADE) = Area(ΔABC)
In ΔADE and ΔABC,
∠ADE = ∠B ...(corresponding angles)
∠A = ∠A
Therefore, ΔADE ∼ ΔABC
∴ `"area(Δ ADE)"/"area(Δ ABC)" = "AD"^2/"AB"^2`
⇒ `"area(ΔADE)"/(2" x area(ΔADE)") = "AD"^2/"AB"^2`
⇒ `(1)/(2) = ("AD"/"AB")^2`
⇒ `"AD"/"AB" = (1)/sqrt(2)`
⇒ AB = `sqrt(2)"AD"`
⇒ AB = `sqrt(2)("AB - BD")`
⇒ `(sqrt(2) - 1)"AB" = sqrt(2)"BD"`
⇒ `"BD"/"AB" = (sqrt(2) - 1)/(sqrt(2)`
= `(2 - sqrt(2))/(2)`.
APPEARS IN
संबंधित प्रश्न
In figure, considering triangles BEP and CPD, prove that BP × PD = EP × PC.
P and Q are points on sides AB and AC respectively of ∆ABC. If AP = 3 cm, PB = 6cm. AQ = 5 cm and QC = 10 cm, show that BC = 3PQ.
In the following figure, if LM || CB and LN || CD, prove that `("AM")/("AB")=("AN")/("AD")`

Two chords AB and CD of a circle intersect at a point P outside the circle.
Prove that: (i) Δ PAC ~ Δ PDB (ii) PA. PB = PC.PD

State the AA-similarity criterion
A triangle LMN has been reduced by scale factor 0.8 to the triangle L' M' N'. Calculate: the length of LM, if L' M' = 5.4 cm.
In ΔABC, point D divides AB in the ratio 5:7, Find: `"AE"/"AC"`
The sides PQ and PR of the ΔPQR are produced to S and T respectively. ST is drawn parallel to QR and PQ: PS = 3:4. If PT = 9.6 cm, find PR. If 'p' be the length of the perpendicular from P to QR, find the length of the perpendicular from P to ST in terms of 'p'.
Find the scale factor in each of the following and state the type of size transformation:
Image length = 6cm, Actual length = 4cm.
Observe the figure and complete the following activity

In fig, ∠B = 75°, ∠D = 75°
∠B ≅ [ ______ ] ...[each of 75°]
∠C ≅ ∠C ...[ ______ ]
ΔABC ~ Δ [ ______ ] ...[ ______ similarity test]
