Advertisements
Advertisements
प्रश्न
Two chords AB and CD of a circle intersect at a point P outside the circle.
Prove that: (i) Δ PAC ~ Δ PDB (ii) PA. PB = PC.PD

उत्तर
Given : AB and CD are two chords
To Prove:
(a) Δ PAC - Δ PDB
(b) PA. PB = PC.PD
Proof: ∠𝐴𝐵𝐷 + ∠𝐴𝐶𝐷 = 180° …(1) (Opposite angles of a cyclic quadrilateral are
supplementary)
∠𝑃𝐶𝐴 + ∠𝐴𝐶𝐷 = 180° …(2) (Linear Pair Angles )
Using (1) and (2), we get
∠𝐴𝐵𝐷 = ∠𝑃𝐶𝐴
∠𝐴 = ∠𝐴 (Common)
By AA similarity-criterion Δ PAC - Δ PDB
When two triangles are similar, then the rations of the lengths of their corresponding sides are proportional
`∴ (PA)/(PD)=(PC)/(PB)`
⟹ PA.PB = PC.PD
APPEARS IN
संबंधित प्रश्न
In the figure given below, Ray PT is bisector of ∠QPR. If PQ = 5.6 cm, QT = 4 cm and TR = 5 cm, find the value of x .

In figure, considering triangles BEP and CPD, prove that BP × PD = EP × PC.
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC in L and AD produced in E. Prove that EL = 2 BL
In figure, ABCD is a trapezium with AB || DC. If ∆AED is similar to ∆BEC, prove that AD = BC.
E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR:
PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
In the following figure, seg DH ⊥ seg EF and seg GK ⊥ seg EF. If DH = 18 cm, GK = 30 cm and `A(triangle DEF) = 450 cm^2`, then find:
1) EF
2) `A(triangle GFE)`
3) `A(square DFGE)`

The perimeters of two similar triangles are 25 cm and 15 cm respectively. If one side of first triangle is 9 cm, what is the corresponding side of the other triangle?
Area of two similar triangles are 98 sq. cm and 128 sq. cm. Find the ratio between the lengths of their corresponding sides.
In the given figure, ABC is a triangle. DE is parallel to BC and `(AD)/(DB) = 3/2`.
- Determine the ratios `(AD)/(AB)` and `(DE)/(BC)`.
- Prove that ∆DEF is similar to ∆CBF. Hence, find `(EF)/(FB).`
- What is the ratio of the areas of ∆DEF and ∆BFC?
In the given figure, DE║BC and DE: BC = 3:5. Calculate the ratio of the areas of ΔADE and the trapezium BCED.

In the given figure, ∠ABC = 75°, ∠EDC = 75° state which two triangles are similar and by which test? Also write the similarity of these two triangles by a proper one to one correspondence.

In the given figure, A – D – C and B – E – C seg DE || side AB If AD = 5, DC = 3, BC = 6.4 then Find BE.

A model of a ship is made with a scale factor of 1 : 500. Find
The deck area of the model, if the deck area of the ship is 1500000 m2
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find:
The number of kilometres on the ground represented by lcm or the map
The scale of a map is 1 : 200000. A plot of land of area 20km2 is to be represented on the map. Find
The area on the map that represents the plot of land.
A triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A' B' C'. Calculate : the length of AB, if A' B' = 6 cm.
A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : OA, if OA' = 6 cm.
In fig.DE || BC ,AD = 1 cm and BD = 2 cm. what is the ratio of the ar(ΔABC) to the ar (ΔADE)?

In the adjoining figure, the medians BD and CE of a ∆ABC meet at G. Prove that
(i) ∆EGD ∼ ∆CGB and
(ii) BG = 2GD for (i) above.
In ΔABC, point D divides AB in the ratio 5:7, Find: DE, If BC = 4.8cm
Harmeet is 6 feet tall and casts a shadow of 3 feet long. What is the height of a nearby pole if it casts a shadow of 12 feet long at the same time?
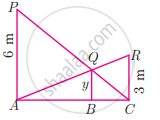
Two vertical poles of heights 6 m and 3 m are erected above a horizontal ground AC. Find the value of y
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that b2 = `"p"^2 + "a"x + "a"^2/4`
A man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4 m from the mirror B, he can see the reflection of the top of the tree. How height is the tree?
In the figure, which of the following statements is true?
Are triangles in figure similar? If yes, then write the test of similarity.
In fig., seg AC and seg BD intersect each other at point P.

`"AP"/"PC" = "BP"/"PD"` then prove that ΔABP ~ ΔCDP
In the given figure ΔABC ~ ΔPQR. The value of x is
 |
 |
Prove that if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.
Using the above theorem prove that a line through the point of intersection of the diagonals and parallel to the base of the trapezium divides the non-parallel sides in the same ratio.
