Advertisements
Advertisements
प्रश्न
In ΔABC, point D divides AB in the ratio 5:7, Find: DE, If BC = 4.8cm
उत्तर
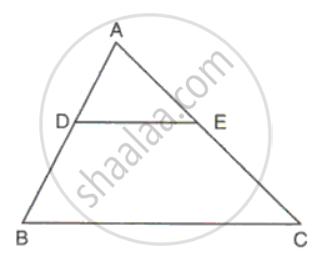
Considering DE || BC
Since DE || BC
`"AD"/"AB" = "DE"/"BC"`
⇒ `(5)/(12) = "DE"/(4.8)`
⇒ DE = `(5 xx 4.8)/(12)`
⇒ BC = 2cm.
APPEARS IN
संबंधित प्रश्न
D is a point on the side BC of ∆ABC such that ∠ADC = ∠BAC. Prove that` \frac{"CA"}{"CD"}=\frac{"CB"}{"CA"} or "CA"^2 = "CB" × "CD".`
E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR.
PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
In the given figure, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC ∼ ΔPDB
(ii) PA.PB = PC.PD

`triangleDEF ~ triangleMNK`. If DE = 5 and MN = 6, then find the value of `(A(triangleDEF))/(A(triangleMNK))`
In the following figure, point D divides AB in the ratio 3 : 5. Find :
BC = 4.8 cm, find the length of DE.

In ΔABC, point D divides AB in the ratio 5:7, Find: `"AE"/"AC"`
The areas of two similar triangles are 16cm2 and 9cm2 respectively. If the altitude of the smaller triangle is 1.8cm, find the length of the altitude corresponding to the larger triangle.
Find the scale factor in each of the following and state the type of size transformation:
Image length = 8cm, Actual length = 20cm.
A vertical stick of length 6 m casts a shadow 400 cm long on the ground and at the same time a tower casts a shadow 28 m long. Using similarity, find the height of the tower
If ∆ABC ~ ∆QRP, `(ar(ABC))/(ar(PQR)) = 9/4`, AB = 18 cm and BC = 15 cm, then PR is equal to ______.
