Advertisements
Advertisements
Question
In ΔABC, point D divides AB in the ratio 5:7, Find: DE, If BC = 4.8cm
Solution
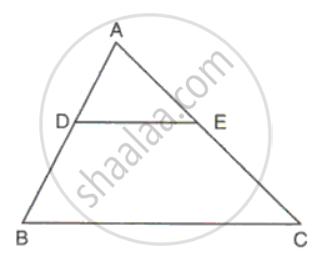
Considering DE || BC
Since DE || BC
`"AD"/"AB" = "DE"/"BC"`
⇒ `(5)/(12) = "DE"/(4.8)`
⇒ DE = `(5 xx 4.8)/(12)`
⇒ BC = 2cm.
APPEARS IN
RELATED QUESTIONS
Area of two similar triangles are 98 sq. cm and 128 sq. cm. Find the ratio between the lengths of their corresponding sides.
In the given figure, BC is parallel to DE. Area of triangle ABC = 25 cm2, Area of trapezium BCED = 24 cm2 and DE = 14 cm. Calculate the length of BC. Also, find the area of triangle BCD.

In the given figure, ΔOAB ~ ΔOCD. If AB = 8cm, BO = 6.4cm, OC = 3.5cm and CD = 5cm, find (i) OA (ii) DO.
In the given figure, ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1cm, PB = 3cm, AQ = 1.5cm, QC = 4.5cm, prove that area of ΔAPQ is 116 of the area of ΔABC.
In Δ ABC , MN || BC .

If BC = 14 cm and MN = 6 cm , find `("Ar" triangle "AMN")/("Ar" . ("trapezium MBCN"))`
Δ ABC ∼ Δ PQR such that AB= 1.5 cm and PQ=2. 1 cm. Find the ratio of areas of Δ ABC and ΔPQR.
PQ is perpendicular to BA and BD is perpendicular to AP.PQ and BD intersect at R. Prove that ΔABD ∼ ΔAPQ and `"AB"/"AP" = "BD"/"PQ"`.
A map is drawn to scale of 1:20000. Find: The distance covered by 6cm on the map
A model of a ship is made to a scale of 1:500. Find: The volume of the model when the volume of the ship is 1km3
Are triangles in figure similar? If yes, then write the test of similarity.
