Advertisements
Advertisements
प्रश्न
In ΔABC, point D divides AB in the ratio 5:7, Find: DE, If BC = 4.8cm
उत्तर
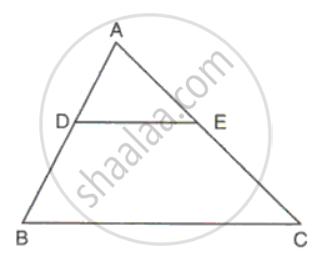
Considering DE || BC
Since DE || BC
`"AD"/"AB" = "DE"/"BC"`
⇒ `(5)/(12) = "DE"/(4.8)`
⇒ DE = `(5 xx 4.8)/(12)`
⇒ BC = 2cm.
APPEARS IN
संबंधित प्रश्न
Examine each pair of triangles in Figure, and state which pair of triangles are similar. Also, state the similarity criterion used by you for answering the question and write the similarity relation in symbolic form
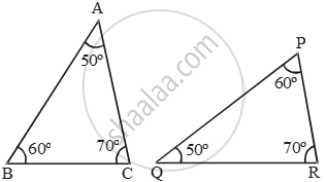
figure (i)
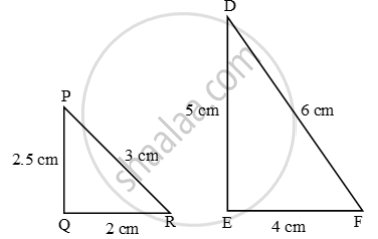
figure 2
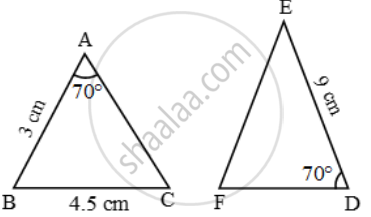
figure 3

figure 4
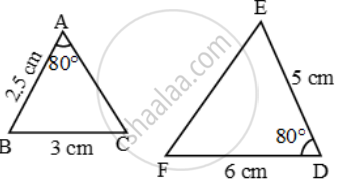
figure 5
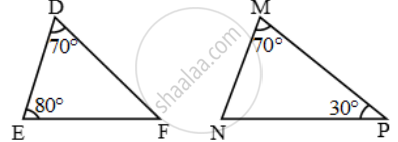
figure 6

figure 7
The diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the side BC. Prove that DF × EF = FB × FA
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC in L and AD produced in E. Prove that EL = 2 BL
State, true or false:
Two isosceles-right triangles are similar.
Area of two similar triangles are 98 sq. cm and 128 sq. cm. Find the ratio between the lengths of their corresponding sides.
In ∆ABC, ray BD bisects ∠ABC and ray CE bisects ∠ACB. If seg AB ≅ seg AC then prove that ED || BC.
In ΔPQR, PQ = 10 cm, QR = 12cm, PR = 8 cm, find the biggest and the smallest angle of the triangle.
Equilateral triangles are drawn on the sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
Two figures are similar. If the ratio of their perimeters is 8:16. What will be the ratio of the corresponding sides?
The ratio of the corresponding altitudes of two similar triangles is `3/5`. Is it correct to say that ratio of their areas is `6/5`? Why?
