Advertisements
Advertisements
Question
In ΔABC, point D divides AB in the ratio 5:7, Find: BC, If DE = 2.5cm
Solution
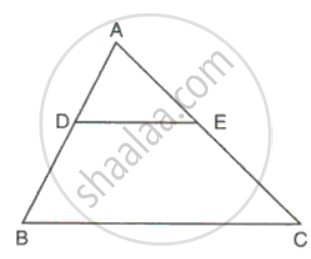
Considering DE || BC
Since DE || BC
`"AD"/"AB" = "DE"/"BC"`
⇒ `(5)/(12) = (2.5)/"BC"`
⇒ BC = `(2.5 xx 12)/(5)`
⇒ BC = 6cm.
APPEARS IN
RELATED QUESTIONS
In an isosceles ∆ABC, the base AB is produced both ways in P and Q such that AP × BQ = AC2 and CE are the altitudes. Prove that ∆ACP ~ ∆BCQ.
See the given figure. DE || BC. Find AD.

In ΔPQR, MN is parallel to QR and `(PM)/(MQ) = 2/3`
1) Find `(MN)/(QR)`
2) Prove that ΔOMN and ΔORQ are similar.
3) Find, Area of ΔOMN : Area of ΔORQ

In an isosceles ΔABC, the base AB is produced both ways in P and Q such that
AP × BQ = AC2.
Prove that ΔACP~ΔBCQ.

In a circle, two chords AB and CD intersect at a point P inside the circle. Prove that
(a) ΔPAC ∼PDB (b) PA. PB= PC.PD

A triangle LMN has been reduced by scale factor 0.8 to the triangle L' M' N'. Calculate: the length of M' N', if MN = 8 cm.
In the following figure, point D divides AB in the ratio 3 : 5. Find : `(AE)/(AC)`

The areas of two similar triangles are 169cm2 and 121cm2 respectively. If one side of the larger triangle is 26cm, find the length of the corresponding side of the smaller triangle.
If ∆ABC – ∆PQR in which ∠A = 53° and ∠Q = 77°, then ∠R is
Areas of two similar triangles are equal then prove that triangles are congruent
