Advertisements
Advertisements
Question
In ΔABC, point D divides AB in the ratio 5:7, Find: `"AE"/"AC"`
Solution
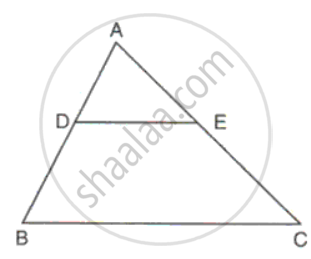
Considering BE || BC
`"AD"/"DB" = "AE"/"EC"`
⇒ `"AE"/"EC" = "AD"/"DB"`
⇒ `"AE"/"EC" =(5)/(7)`
∵ AC = AE + EC
⇒ AC
= 5 + 7
= 12
∴ `"AE"/"AC" = (5)/(12)` .
APPEARS IN
RELATED QUESTIONS
If a perpendicular is drawn from the vertex containing the right angle of a right triangle to the hypotenuse then prove that the triangle on each side of the perpendicular are similar to each other and to the original triangle. Also, prove that the square of the perpendicular is equal to the product of the lengths of the two parts of the hypotenuse
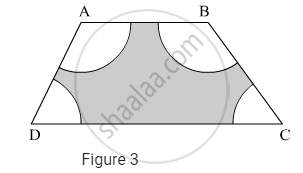
In Figure 3, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and the distance between AB and DC is 14 cm. If arcs of equal radii 7 cm have been drawn, with centres A,B, C and D, then find the area of the shaded region.
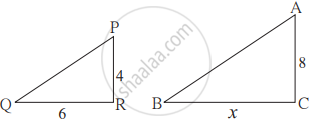
As shown in figure, two poles of height 8 m and 4 m are perpendicular to the ground. If the length of shadow of smaller pole due to sunlight is 6 m then how long will be the shadow of the bigger pole at the same time?
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 8cm, AB = 12cm and AE = 12cm, find CE.
Find the scale factor in each of the following and state the type of size transformation:
Actual area = 64m2, Model area = 100cm2
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The length of the truck
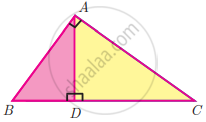
In the adjacent figure ∠BAC = 90° and AD ⊥ BC then
In the given figure AB || CD || EF. If AB = 6 cm, CD = x cm, EF = 4 cm, BD = 5 cm and DE = y cm. Find x and y.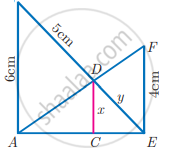
In the figure, if ∠FEG ≡ ∠1 then, prove that DG2 = DE.DF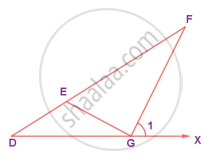
Two triangles are similar. Smaller triangle’s sides are 4 cm, 5 cm, 6 cm. Perimeter of larger triangle is 90 cm then find the sides of larger triangle.
