Advertisements
Advertisements
Question
Areas of two similar triangles are equal then prove that triangles are congruent
Solution
Given: ΔABC ~ ΔPQR and A(ΔABC) = A(ΔPQR)
To prove: ΔABC ≅ ΔPQR
Proof:
`("A"(Δ"ABC"))/("A"(Δ"PQR"))` = 1 ......(i) [Given]
Also, `("A"(Δ"ABC"))/("A"(Δ"PQR")) = "AB"^2/"PQ"^2 = "BC"^2/"QR"^2 = "AC"^2/"PR"^2` ......[Theorem of areas of similar triangles]
∴ 1 = `"AB"^2/"PQ"^2 = "BC"^2/"QR"^2 = "AC"^2/"PR"^2` .....[From (i)]
∴ 1 = `"AB"^2/"PQ"^2`
∴ AB2 = PQ2
∴ AB = PQ ......[Taking square root of both sides]
i.e., seg AB ≅ seg PQ
Similarly, seg BC ≅ seg QR and seg AC ≅ seg PR
∴ ΔABC ≅ ΔPQR ......[SSS test of congruency]
RELATED QUESTIONS
P and Q are points on sides AB and AC respectively of ∆ABC. If AP = 3 cm, PB = 6cm. AQ = 5 cm and QC = 10 cm, show that BC = 3PQ.
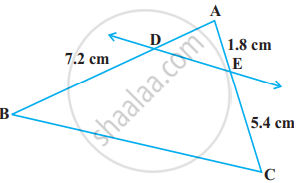
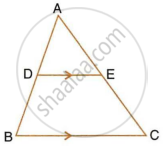
See the given figure. DE || BC. Find AD.
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that `("AO")/("BO") = ("CO")/("DO")`
State, true or false:
Two isosceles-right triangles are similar.
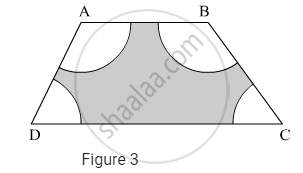
In Figure 3, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and the distance between AB and DC is 14 cm. If arcs of equal radii 7 cm have been drawn, with centres A,B, C and D, then find the area of the shaded region.
In ∆ABC, ray BD bisects ∠ABC and ray CE bisects ∠ACB. If seg AB ≅ seg AC then prove that ED || BC.
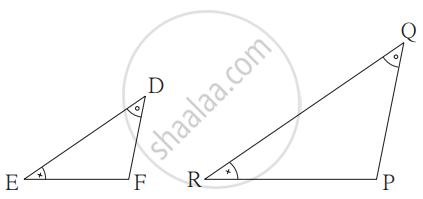
Are the triangles in the given figure similar? If yes, by which test?
If in ∆DEF and ∆PQR, ∠D ≅ ∠Q, ∠R ≅ ∠E then which of the following statements is false?
ΔABC ∼ ΔDEF and A(ΔABC) : A Δ(DEF) = 1 : 2 If AB = 4 find DE.
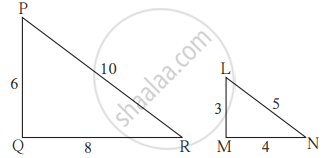
In figure , DEF is a right -angled triangle with ∠ E = 90 °.FE is produced to G and GH is drawn perpendicular to DE = 8 cm , DH = 8 cm ,DH = 6 cm and HF = 4 cm , find `("Ar" triangle "DEF")/("Ar" triangle "GHF")`
In the following figure, point D divides AB in the ratio 3 : 5. Find :
BC = 4.8 cm, find the length of DE.
In the given figure, PQ || AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find : PQ

Construct a ΔABC in which CA = 6 cm, AB = 5 cm and ∠BAC = 45°. Then construct a triangle whose sides are `3/5` of the corresponding sides of ΔABC.
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The diagonal distance of the plot in km
Construct a triangle similar to a given triangle PQR with its sides equal to `2/3` of the corresponding sides of the triangle PQR (scale factor `2/3 < 1`)
In the figure, which of the following statements is true?
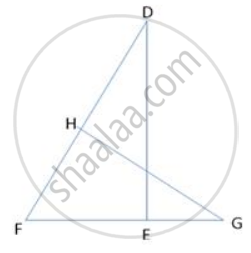
In the figure, if ∠FEG ≡ ∠1 then, prove that DG2 = DE.DF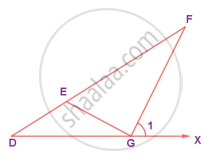
There are two poles having heights 8 m and 4 m on plane ground as shown in fig. Because of sunlight shadows of smaller pole is 6m long, then find the length of shadow of longer pole.
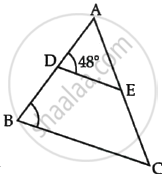
In figure, if AD = 6 cm, DB = 9 cm, AE = 8 cm and EC = 12 cm and ∠ADE = 48°. Find ∠ABC.