Advertisements
Online Mock Tests
Chapters
![SCERT Maharashtra solutions for Geometry (Mathematics 2) [English] 10 Standard SSC chapter 1 - Similarity SCERT Maharashtra solutions for Geometry (Mathematics 2) [English] 10 Standard SSC chapter 1 - Similarity - Shaalaa.com](/images/geometry-mathematics-2-english-10-standard-ssc_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 1: Similarity
Below listed, you can find solutions for Chapter 1 of Maharashtra State Board SCERT Maharashtra for Geometry (Mathematics 2) [English] 10 Standard SSC.
SCERT Maharashtra solutions for Geometry (Mathematics 2) [English] 10 Standard SSC 1 Similarity Q.1 (A)
MCQ [1 Mark]
If ∆ABC ~ ∆PQR and AB : PQ = 3 : 4 then A(∆ABC) : A(∆PQR) = ?
9 : 25
9 : 16
16 : 9
25 : 9
Which of the following is not a test of similarity?
AAA
SAS
SAA
SSS
If ∆XYZ ~ ∆PQR and A(∆XYZ) = 25 cm2, A(∆PQR) = 4 cm2 then XY : PQ = ?
4 : 25
2 : 5
5 : 2
25 : 4
Ratio of areas of two similar triangles is 9 : 25. _______ is the ratio of their corresponding sides.
3 : 4
3 : 5
5 : 3
25 : 81
Given ΔABC ~ ΔDEF, if ∠A = 45° and ∠E = 35° then ∠B = ?
45°
35°
25°
40°
In fig, seg DE || sec BC, identify the correct statement.
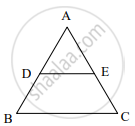
`"AD"/"DB" = "AE"/"AC"`
`"AD"/"DB" = "AB"/"AC"`
`"AD"/"DB" = "EC"/"AC"`
`"AD"/"DB" = "AE"/"EC"`
If ΔXYZ ~ ΔPQR then `"XY"/"PQ" = "YZ"/"QR"` = ?
`"XZ"/"PR"`
`"XZ"/"PQ"`
`"XZ"/"QR"`
`"YZ"/"PQ"`
If ΔABC ~ ΔLMN and ∠A = 60° then ∠L = ?
45°
60°
25°
40°
In ΔDEF and ΔXYZ, `"DE"/"XY" = "FE"/"YZ"` and ∠E ≅ ∠Y. _______ test gives similarity between ΔDEF and ΔXYZ.
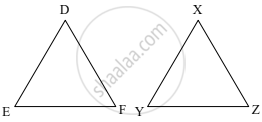
AAA
SAS
SAA
SSS
In fig. BD = 8, BC = 12, B-D-C, then `"A(ΔABC)"/"A(ΔABD)"` = ?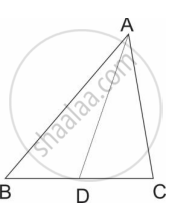
2 : 3
3 : 2
5 : 3
3 : 4
SCERT Maharashtra solutions for Geometry (Mathematics 2) [English] 10 Standard SSC 1 Similarity Q.1 (B)
Solve [1 Mark]
Are triangles in figure similar? If yes, then write the test of similarity.
In fig., line BC || line DE, AB = 2, BD = 3, AC = 4 and CE = x, then find the value of x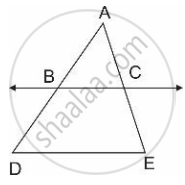
State whether the following triangles are similar or not: If yes, then write the test of similarity.
∠P = 35°, ∠X = 35° and ∠Q = 60°, ∠Y = 60°

If ΔABC ~ ΔLMN and ∠B = 40°, then ∠M = ? Give reason.
Areas of two similar triangles are in the ratio 144: 49. Find the ratio of their corresponding sides.
ΔPQR ~ ΔSUV. Write pairs of congruent angles
ΔABC ~ ΔDEF. Write the ratios of their corresponding sides
In fig., TP = 10 cm, PS = 6 cm. `"A(ΔRTP)"/"A(ΔRPS)"` = ?
Ratio of corresponding sides of two similar triangles is 4:7, then find the ratio of their areas = ?
Write the test of similarity for triangles given in figure.
SCERT Maharashtra solutions for Geometry (Mathematics 2) [English] 10 Standard SSC 1 Similarity Q.2 (A)
Complete the activity [2 Marks]
In fig. BP ⊥ AC, CQ ⊥ AB, A−P−C, and A−Q−B then show that ΔAPB and ΔAQC are similar.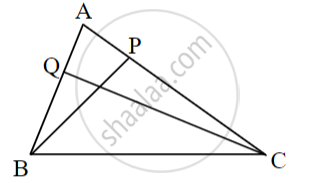
In ΔAPB and ΔAQC
∠APB = [ ]° ......(i)
∠AQC = [ ]° ......(ii)
∠APB ≅ ∠AQC .....[From (i) and (ii)]
∠PAB ≅ ∠QAC .....[______]
ΔAPB ~ ΔAQC .....[______]
Observe the figure and complete the following activity
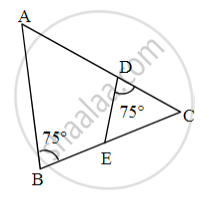
In fig, ∠B = 75°, ∠D = 75°
∠B ≅ [ ______ ] ...[each of 75°]
∠C ≅ ∠C ...[ ______ ]
ΔABC ~ Δ [ ______ ] ...[ ______ similarity test]
ΔABC ~ ΔPQR, A(ΔABC) = 80 sq.cm, A(ΔPQR) = 125 sq.cm, then complete `("A"(Δ"ABC"))/("A"(Δ"PQR")) = 80/125 = (["______"])/(["______"])`, hence `"AB"/"PQ" = (["______"])/(["______"])`
In fig., PM = 10 cm, A(ΔPQS) = 100 sq.cm, A(ΔQRS) = 110 sq.cm, then NR?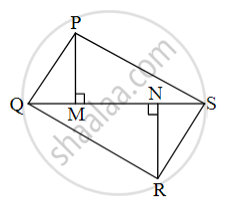
ΔPQS and ΔQRS having seg QS common base.
Areas of two triangles whose base is common are in proportion of their corresponding [______]
`("A"("PQS"))/("A"("QRS")) = (["______"])/"NR"`,
`100/110 = (["______"])/"NR"`,
NR = [ ______ ] cm
SCERT Maharashtra solutions for Geometry (Mathematics 2) [English] 10 Standard SSC 1 Similarity Q.2 (B)
[2 Marks]
In fig., AB ⊥ BC and DC ⊥ BC, AB = 6, DC = 4 then `("A"(Δ"ABC"))/("A"(Δ"BCD"))` = ?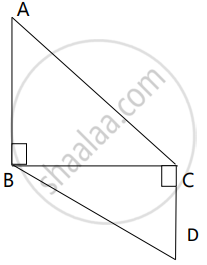
In fig., seg AC and seg BD intersect each other at point P.
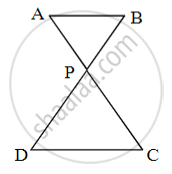
`"AP"/"PC" = "BP"/"PD"` then prove that ΔABP ~ ΔCDP
ΔABP ~ ΔDEF and A(ΔABP) : A(ΔDEF) = 144:81, then AB : DE = ?
From given information, is PQ || BC?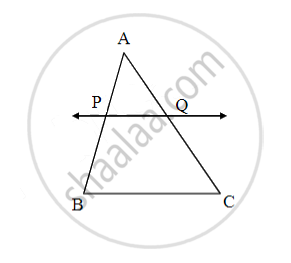
AP = 2, PB = 4, AQ = 3, QC = 6
Areas of two similar triangles are 225 cm2 and 81 cm2. If side of smaller triangle is 12 cm, find corresponding side of major triangle.
From adjoining figure, ∠ABC = 90°, ∠DCB = 90°, AB = 6, DC = 8, then `("A"(Δ"ABC"))/("A"(Δ"BCD"))` = ?

SCERT Maharashtra solutions for Geometry (Mathematics 2) [English] 10 Standard SSC 1 Similarity Q.3 (A)
Complete the following activities [3 Marks]
In ΔABC, AP ⊥ BC and BQ ⊥ AC, B−P−C, A−Q−C, then show that ΔCPA ~ ΔCQB. If AP = 7, BQ = 8, BC = 12, then AC = ?
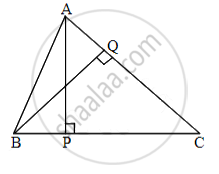
In ΔCPA and ΔCQB
∠CPA ≅ [∠ ______] ...[each 90°]
∠ACP ≅ [∠ ______] ...[common angle]
ΔCPA ~ ΔCQB ......[______ similarity test]
`"AP"/"BQ" = (["______"])/"BC"` .......[corresponding sides of similar triangles]
`7/8 = (["______"])/12`
AC × [______] = 7 × 12
AC = 10.5
A line is parallel to one side of triangle which intersects remaining two sides in two distinct points then that line divides sides in same proportion.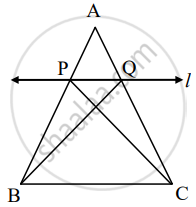
Given: In ΔABC line l || side BC and line l intersect side AB in P and side AC in Q.
To prove: `"AP"/"PB" = "AQ"/"QC"`
Construction: Draw CP and BQ
Proof: ΔAPQ and ΔPQB have equal height.
`("A"(Δ"APQ"))/("A"(Δ"PQB")) = (["______"])/"PB"` .....(i)[areas in proportion of base]
`("A"(Δ"APQ"))/("A"(Δ"PQC")) = (["______"])/"QC"` .......(ii)[areas in proportion of base]
ΔPQC and ΔPQB have [______] is common base.
Seg PQ || Seg BC, hence height of ΔAPQ and ΔPQB.
A(ΔPQC) = A(Δ______) ......(iii)
`("A"(Δ"APQ"))/("A"(Δ"PQB")) = ("A"(Δ "______"))/("A"(Δ "______"))` ......[(i), (ii), and (iii)]
`"AP"/"PB" = "AQ"/"QC"` .......[(i) and (ii)]
From fig., seg PQ || side BC, AP = x + 3, PB = x – 3, AQ = x + 5, QC = x – 2, then complete the activity to find the value of x.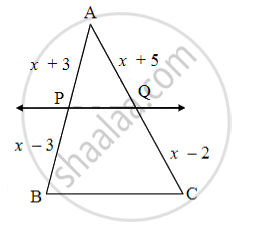
In ΔPQB, PQ || side BC
`"AP"/"PB" = "AQ"/(["______"])` ...[______]
`(x + 3)/(x - 3) = (x + 5)/(["______"])`
(x + 3) [______] = (x + 5)(x – 3)
x2 + x – [______] = x2 + 2x – 15
x = [______]
SCERT Maharashtra solutions for Geometry (Mathematics 2) [English] 10 Standard SSC 1 Similarity Q.3 (B)
[3 Marks]
There are two poles having heights 8 m and 4 m on plane ground as shown in fig. Because of sunlight shadows of smaller pole is 6m long, then find the length of shadow of longer pole.
In ΔABC, B − D − C and BD = 7, BC = 20, then find the following ratio.
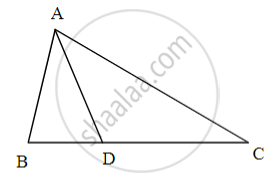
(i) `"A(ΔABD)"/"A(ΔADC)"`
(ii) `"A(ΔABD)"/"A(ΔABC)"`
(iii) `"A(ΔADC)"/"A(ΔABC)"`
In given fig., quadrilateral PQRS, side PQ || side SR, AR = 5 AP, then prove that, SR = 5PQ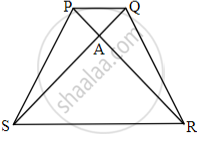
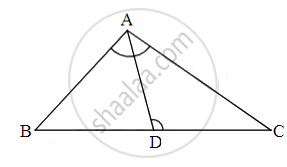
In triangle ABC point D is on side BC (B−D−C) such that ∠BAC = ∠ADC then prove that CA2 = CB × CD
In Quadrilateral ABCD, side AD || BC, diagonal AC and BD intersect in point P, then prove that `"AP"/"PD" = "PC"/"BP"`
SCERT Maharashtra solutions for Geometry (Mathematics 2) [English] 10 Standard SSC 1 Similarity Q.4
[4 Marks]
Side of equilateral triangle PQR is 8 cm then find the area of triangle whose side is half of the side of triangle PQR.
Areas of two similar triangles are equal then prove that triangles are congruent
Two triangles are similar. Smaller triangle’s sides are 4 cm, 5 cm, 6 cm. Perimeter of larger triangle is 90 cm then find the sides of larger triangle.
SCERT Maharashtra solutions for Geometry (Mathematics 2) [English] 10 Standard SSC 1 Similarity Q.5
[3 Marks]
In fig., PS = 2, SQ = 6, QR = 5, PT = x and TR = y. Then find the pair of value of x and y such that ST || side QR.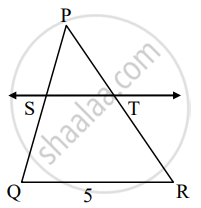
An architecture have model of building. Length of building is 1 m then length of model is 0.75 cm. Then find length and height of model building whose actual length is 22.5 m and height is 10 m
Solutions for 1: Similarity
![SCERT Maharashtra solutions for Geometry (Mathematics 2) [English] 10 Standard SSC chapter 1 - Similarity SCERT Maharashtra solutions for Geometry (Mathematics 2) [English] 10 Standard SSC chapter 1 - Similarity - Shaalaa.com](/images/geometry-mathematics-2-english-10-standard-ssc_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
SCERT Maharashtra solutions for Geometry (Mathematics 2) [English] 10 Standard SSC chapter 1 - Similarity
Shaalaa.com has the Maharashtra State Board Mathematics Geometry (Mathematics 2) [English] 10 Standard SSC Maharashtra State Board solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. SCERT Maharashtra solutions for Mathematics Geometry (Mathematics 2) [English] 10 Standard SSC Maharashtra State Board 1 (Similarity) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. SCERT Maharashtra textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Geometry (Mathematics 2) [English] 10 Standard SSC chapter 1 Similarity are Properties of Ratios of Areas of Two Triangles, Similar Triangles, Areas of Similar Triangles, Basic Proportionality Theorem (Thales Theorem), Property of an Angle Bisector of a Triangle, Property of Three Parallel Lines and Their Transversals, Converse of Basic Proportionality Theorem, Similarity of Triangles, Criteria for Similarity of Triangles.
Using SCERT Maharashtra Geometry (Mathematics 2) [English] 10 Standard SSC solutions Similarity exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in SCERT Maharashtra Solutions are essential questions that can be asked in the final exam. Maximum Maharashtra State Board Geometry (Mathematics 2) [English] 10 Standard SSC students prefer SCERT Maharashtra Textbook Solutions to score more in exams.
Get the free view of Chapter 1, Similarity Geometry (Mathematics 2) [English] 10 Standard SSC additional questions for Mathematics Geometry (Mathematics 2) [English] 10 Standard SSC Maharashtra State Board, and you can use Shaalaa.com to keep it handy for your exam preparation.
