Advertisements
Advertisements
Question
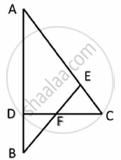
In fig, seg DE || sec BC, identify the correct statement.

Options
`"AD"/"DB" = "AE"/"AC"`
`"AD"/"DB" = "AB"/"AC"`
`"AD"/"DB" = "EC"/"AC"`
`"AD"/"DB" = "AE"/"EC"`
Solution
`"AD"/"DB" = "AE"/"EC"`
Explanation:
In ΔABC,
seg DE || sec BC ...(Given)
∴ By Basic proportionality theorem,
`"AD"/"DB" = "AE"/"EC"`.
RELATED QUESTIONS
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4, AE = 8, DB = x – 4, and EC = 3x – 19, find x.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 2cm, AD = 8cm, AE = 12 cm and AC = l8cm.
In three line segments OA, OB, and OC, points L, M, N respectively are so chosen that LM || AB and MN || BC but neither of L, M, N nor of A, B, C are collinear. Show that LN ||AC.
If D and E are points on sides AB and AC respectively of a ΔABC such that DE || BC and BD = CE. Prove that ΔABC is isosceles.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AB = 13.3cm, AC = 11.9cm and EC = 5.1cm, find AD.
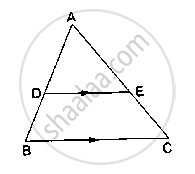
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If `(AD)/(DB) = 4/7` and AC = 6.6cm, find AE.
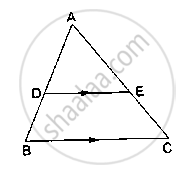
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If` (AD)/(AB) = 8/15 and EC = 3.5cm`, find AE.
Show that the line segment which joins the midpoints of the oblique sides of a trapezium is parallel sides
Two vertical poles of height 9m and 14m stand on a plane ground. If the distance between their feet is 12m, find the distance between their tops.
In the given figure, O is a point inside a ΔPQR such that ∠PQR such that ∠POR = 90°, OP = 6cm and OR = 8cm. If PQ = 24cm and QR = 26cm, prove that ΔPQR is right-angled.
In a ABC , AD is a median and AL ⊥ BC .
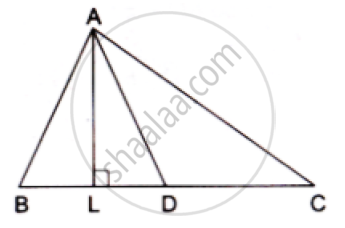
Prove that
(a) `AC^2=AD^2+BC DL+((BC)/2)^2`
(b) `AB^2=AD^2-BC DL+((BC)/2)^2`
(c) `AC^2+AB^2=2.AD^2+1/2BC^2`
In triangle BMP and CNR it is given that PB= 5 cm, MP = 6cm BM = 9 cm and NR = 9cm. If ΔBMP∼ ΔCNR then find the perimeter of ΔCNR
◻ABCD is a parallelogram point E is on side BC. Line DE intersects ray AB in point T. Prove that DE × BE = CE × TE.

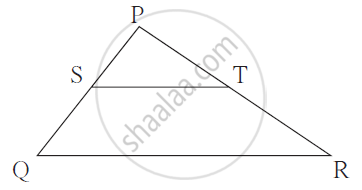
In Δ PQR, points S and T
are the midpoints of sides PQ
and PR respectively.
If ST = 6.2 then find the length of QR.
In fig., PS = 2, SQ = 6, QR = 5, PT = x and TR = y. Then find the pair of value of x and y such that ST || side QR.
O is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB || DC. Through O, a line segment PQ is drawn parallel to AB meeting AD in P and BC in Q. Prove that PO = QO.
In figure, line segment DF intersect the side AC of a triangle ABC at the point E such that E is the mid-point of CA and ∠AEF = ∠AFE. Prove that `(BD)/(CD) = (BF)/(CE)`.
In the given figure ∠CEF = ∠CFE. F is the midpoint of DC. Prove that `(AB)/(BD) = (AE)/(FD)`