Advertisements
Advertisements
Question
Show that the line segment which joins the midpoints of the oblique sides of a trapezium is parallel sides
Solution
Let the trapezium be ABCD with E and F as the mid Points of AD and BC, Respectively Produce AD and BC to Meet at P.
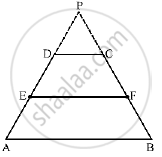
In Δ PAB, DC || AB.
Applying Thales’ theorem, we get
`(PD)/(DA)=(PC)/(CB)`
Now, E and F are the midpoints of AD and BC, respectively
⇒ `(PD)/(2DE)=(PC)/(2CF)`
⟹ `(PD)/(DE)=(PC)/(CF)`
Applying the converse of Thales’ theorem in Δ PEF, we get that DC
Hence, EF || AB.
Thus. EF is parallel to both AB and DC.
This completes the proof.
APPEARS IN
RELATED QUESTIONS
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 5.6cm, AD = 1.4cm, AC= 7.2 cm and AE = 1.8 cm.
In below Fig., state if PQ || EF.
In three line segments OA, OB, and OC, points L, M, N respectively are so chosen that LM || AB and MN || BC but neither of L, M, N nor of A, B, C are collinear. Show that LN ||AC.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AB = 13.3cm, AC = 11.9cm and EC = 5.1cm, find AD.
ΔABC is an isosceles triangle with AB = AC = 13cm. The length of altitude from A on BC is 5cm. Find BC.
ΔABC is am equilateral triangle of side 2a units. Find each of its altitudes.
State the basic proportionality theorem.
ABCD is a trapezium in which AB || DC and P and Q are points on AD and BC, respectively such that PQ || DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD.
Prove that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. In the figure, find EC if `(AD)/(DB) = (AE)/(EC)` using the above theorem.

In the given figure, PQ || AC. If BP = 4 cm, AP = 2.4 cm and BQ = 5 cm, then length of BC is ______.

