Advertisements
Advertisements
Question
Prove that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. In the figure, find EC if `(AD)/(DB) = (AE)/(EC)` using the above theorem.

Solution
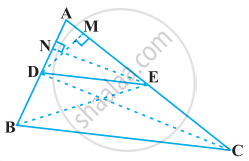
Proof: We are given a triangle ABC in which a line parallel to side BC intersects the other two sides AB and AC at D and E respectively.
We need to prove that `(AD)/(DB) = (AE)/(EC)`
Let us join BE and CD and then draw DM ⊥ AC and EN ⊥ AB.
Now, area of ∆ADE = `1/2` (base × height) = `1/2` AD × EN
The area of ∆ADE is denoted as ar(ADE).
So, ar(ADE) = `1/2` AD × EN
Similarly, ar(BDE) = `1/2` DB × EN,
ar(ADE) = `1/2` AE × DM and ar(DEC) = `1/2` EC × DM
Therefore, `(ar(ADE))/(ar(BDE)) = (1/2 AD xx EN)/(1/2 DB xx EN) = (AD)/(DB)` ......(1)
And `(ar(ADE))/(ar(DEC)) = (1/2 AE xx DM)/(1/2 EC xx DM) = (AE)/(EC)` ......(2)
Note that ∆BDE and DEC are on the same base DE and between the same parallels BC and DE.
So, ar(BDE) = ar(DEC) ......(3)
Therefore, from (1), (2) and (3), we have:
`(AD)/(DB) = (AE)/(EC)`
APPEARS IN
RELATED QUESTIONS
In the following figure, DE || AC and DF || AE. Prove that `("BF")/("FE") = ("BE")/("EC")`

In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8x − 7, DB = 5x − 3, AE = 4x − 3 and EC = (3x − 1), find the value of x.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4x − 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x − 3, find the volume of x.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and EC = 5.5 cm.
In three line segments OA, OB, and OC, points L, M, N respectively are so chosen that LM || AB and MN || BC but neither of L, M, N nor of A, B, C are collinear. Show that LN ||AC.
In the given figure, ABCD is a trapezium in which AB║DC and its diagonals intersect at O. If AO = (5x – 7), OC = (2x + 1) , BO = (7x – 5) and OD = (7x + 1), find the value of x.

Find the height of an equilateral triangle of side 12cm.
An aeroplane leaves an airport and flies due north at a speed of 1000km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after` 1 1/2` hours?
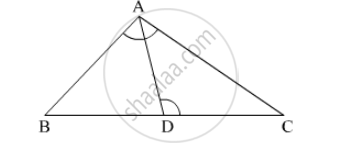
In the given figure, in ∆ABC, point D on side BC is such that, ∠BAC = ∠ADC. Prove that, CA2 = CB × CD
Prove that, if a line parallel to a side of a triangle intersects the other sides in two district points, then the line divides those sides in proportion.
