Advertisements
Advertisements
Questions
Prove that, if a line parallel to a side of a triangle intersects the other sides in two district points, then the line divides those sides in proportion.
Prove that, 'If a line parallel to a side of a triangle intersects the remaining sides in two distinct points, then the line divides the side in the same proportion’.
Solution 1
Given: A Δ ABC in which DE||BC, and intersect AB in D and AC in E.
To Prove: `"AD"/"BD" = "AE"/"EC"`
Construction: Join BE, CD, and draw EF⊥ BA and DG⊥CA.

Proof:
Area ∆ADE = `1/2 xx ("base" xx "height") =1/2("AD. EF")`
Area ∆DBE = `1/2 xx("base" xx "height") =1/2("DB.EF")`
⇒ `("Area"(triangle"ADE"))/("Area"(triangle"DBE"))=[((1/2"AD. EF"))/((1/2"DB. EF")]] = "AD"/"DB"`
Similarly,
⇒ `("Area"(triangle"ADE"))/("Area"(triangle"DBE"))=[((1/2"AE. DG"))/((1/2"EC. DG")]] = "AE"/"EC"`
ΔDBE and ΔDEC are on the same base DE and BC the same parallel DE and BC.
∴ Area (ΔDBE) = Area (ΔDEC)
⇒ `1/("Area"(triangle"DBE")) =1/("Area"(triangle"DEC"))` ...[Taking reciprocal of both sides]
⇒ `("Area"(triangle"ADE"))/("Area"(triangle"DBE"))=("Area"(triangle"ADE"))/("Area"(triangle"DEC")` ...[Multiplying both sides by Area (ΔADE)]
⇒ `"AD"/"DB"="AE"/"EC"`
Hence Proved.
Solution 2
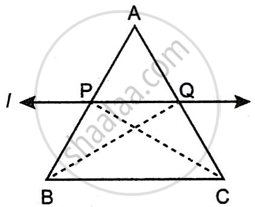
Given: In Δ ABC line l || line BC and line l intersects AB and AC in point P and Q respectively.
To prove: `"AP"/"PB" = "AQ"/"QC"`
Construction: Draw seg PC and seg BQ.
Proof: ΔAPQ and ΔPQB have equal heights.
`therefore ("A"(Delta "APQ"))/("A"(Delta "PQB")) = "AP"/"PB"` (areas proportionate to bases) ...(I)
and `("A"(Delta "APQ"))/("A"(Delta "PQC")) = "AQ"/"QC"` (areas proportionate to bases) ...(II)
Seg PQ is the common base of ΔPQB and ΔPQC, seg PQ || seg BC,
Hence ΔPQB and ΔPQC have equal areas.
A(ΔPQB) = A(ΔPQC) ...(III)
`("A"(Delta "APQ"))/("A"(Delta "PQB")) = ("A"(Delta "APQ"))/("A"(Delta "PQC"))` ...[from (I), (II) and (III)]
`therefore "AP"/"PB" = "AQ"/"QC"` ...[from (I) and (II)]
Hence Proved.
RELATED QUESTIONS
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8cm, AB = 12 cm and AE = 12 cm, find CE.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"BD"=4/5` and EC = 2.5 cm, find AE
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8x − 7, DB = 5x − 3, AE = 4x − 3 and EC = (3x − 1), find the value of x.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 2cm, AD = 8cm, AE = 12 cm and AC = l8cm.
M and N are points on the sides PQ and PR respectively of a ΔPQR. For the following case, state whether MN || QR
PM = 4cm, QM = 4.5 cm, PN = 4 cm and NR = 4.5 cm
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = x cm, DB = (x – 2) cm, AE = (x + 2) cm and EC = (x – 1) cm.
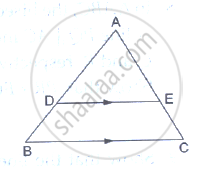
ΔABC and ΔDBC lie on the same side of BC, as shown in the figure. From a point P on BC, PQ||AB and PR||BD are drawn, meeting AC at Q and CD at R respectively. Prove that QR||AD.
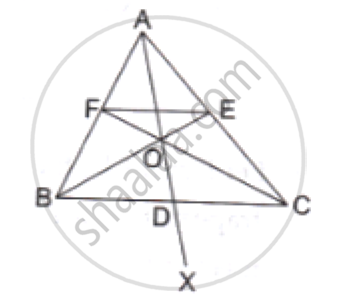
ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that CQ = `1/4` AC. If PQ produced meets BC at R, prove that R is the midpoint of BC.

A guy wire attached to a vertical pole of height 18 m is 24m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Find the length of a diagonal of a rectangle whose adjacent sides are 30cm and 16cm.
In the given figure, ∠ACB 90° CD ⊥ AB Prove that `(BC^2)/(AC^2)=(BD)/(AD)`

In the given figure, D is the midpoint of side BC and AE⊥BC. If BC = a, AC = b, AB = c, AD = p and AE = h, prove that
(i)`B^2=p^2+ax+a^2/x`
(ii)` c^2=p^2-ax+a^2/x`
(iii) `b^2+c^2=2p^2+a^2/2`
(iv)`b^2-c^2=2ax`

An aeroplane leaves an airport and flies due north at a speed of 1000km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after` 1 1/2` hours?
In a ABC , AD is a median and AL ⊥ BC .
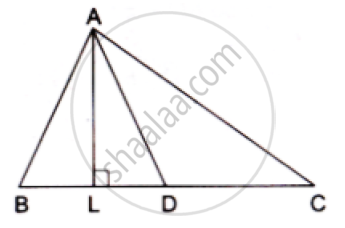
Prove that
(a) `AC^2=AD^2+BC DL+((BC)/2)^2`
(b) `AB^2=AD^2-BC DL+((BC)/2)^2`
(c) `AC^2+AB^2=2.AD^2+1/2BC^2`
In triangle BMP and CNR it is given that PB= 5 cm, MP = 6cm BM = 9 cm and NR = 9cm. If ΔBMP∼ ΔCNR then find the perimeter of ΔCNR
Each of the equal sides of an isosceles triangle is 25 cm. Find the length of its altitude if the base is 14 cm.
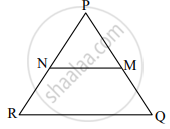
In ΔPQR, NM || RQ. If PM = 15, MQ = 10, NR = 8, then find PN.
In fig., PS = 2, SQ = 6, QR = 5, PT = x and TR = y. Then find the pair of value of x and y such that ST || side QR.
Construct an equilateral triangle of side 7 cm. Now, construct another triangle similar to the first triangle such that each of its sides are `5/7` times of the corresponding sides of the first triangle.
