Advertisements
Advertisements
प्रश्न
Prove that, if a line parallel to a side of a triangle intersects the other sides in two district points, then the line divides those sides in proportion.
Prove that, 'If a line parallel to a side of a triangle intersects the remaining sides in two distinct points, then the line divides the side in the same proportion’.
उत्तर १
Given: A Δ ABC in which DE||BC, and intersect AB in D and AC in E.
To Prove: `"AD"/"BD" = "AE"/"EC"`
Construction: Join BE, CD, and draw EF⊥ BA and DG⊥CA.

Proof:
Area ∆ADE = `1/2 xx ("base" xx "height") =1/2("AD. EF")`
Area ∆DBE = `1/2 xx("base" xx "height") =1/2("DB.EF")`
⇒ `("Area"(triangle"ADE"))/("Area"(triangle"DBE"))=[((1/2"AD. EF"))/((1/2"DB. EF")]] = "AD"/"DB"`
Similarly,
⇒ `("Area"(triangle"ADE"))/("Area"(triangle"DBE"))=[((1/2"AE. DG"))/((1/2"EC. DG")]] = "AE"/"EC"`
ΔDBE and ΔDEC are on the same base DE and BC the same parallel DE and BC.
∴ Area (ΔDBE) = Area (ΔDEC)
⇒ `1/("Area"(triangle"DBE")) =1/("Area"(triangle"DEC"))` ...[Taking reciprocal of both sides]
⇒ `("Area"(triangle"ADE"))/("Area"(triangle"DBE"))=("Area"(triangle"ADE"))/("Area"(triangle"DEC")` ...[Multiplying both sides by Area (ΔADE)]
⇒ `"AD"/"DB"="AE"/"EC"`
Hence Proved.
उत्तर २
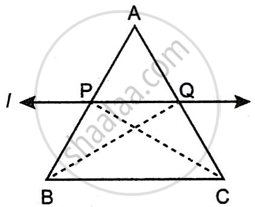
Given: In Δ ABC line l || line BC and line l intersects AB and AC in point P and Q respectively.
To prove: `"AP"/"PB" = "AQ"/"QC"`
Construction: Draw seg PC and seg BQ.
Proof: ΔAPQ and ΔPQB have equal heights.
`therefore ("A"(Delta "APQ"))/("A"(Delta "PQB")) = "AP"/"PB"` (areas proportionate to bases) ...(I)
and `("A"(Delta "APQ"))/("A"(Delta "PQC")) = "AQ"/"QC"` (areas proportionate to bases) ...(II)
Seg PQ is the common base of ΔPQB and ΔPQC, seg PQ || seg BC,
Hence ΔPQB and ΔPQC have equal areas.
A(ΔPQB) = A(ΔPQC) ...(III)
`("A"(Delta "APQ"))/("A"(Delta "PQB")) = ("A"(Delta "APQ"))/("A"(Delta "PQC"))` ...[from (I), (II) and (III)]
`therefore "AP"/"PB" = "AQ"/"QC"` ...[from (I) and (II)]
Hence Proved.
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = x, DB = x − 2, AE = x + 2 and EC = x − 1, find the value of x.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 2cm, AD = 8cm, AE = 12 cm and AC = l8cm.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and EC = 5.5 cm.
If D and E are points on sides AB and AC respectively of a ΔABC such that DE || BC and BD = CE. Prove that ΔABC is isosceles.
D and E are the points on the sides AB and AC respectively of a ΔABC such that: AD = 8 cm, DB = 12 cm, AE = 6 cm and CE = 9 cm. Prove that BC = 5/2 DE.
Two vertical poles of height 9m and 14m stand on a plane ground. If the distance between their feet is 12m, find the distance between their tops.
A guy wire attached to a vertical pole of height 18 m is 24m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
In the given figure, O is a point inside a ΔPQR such that ∠PQR such that ∠POR = 90°, OP = 6cm and OR = 8cm. If PQ = 24cm and QR = 26cm, prove that ΔPQR is right-angled.
ΔABC is an isosceles triangle with AB = AC = 13cm. The length of altitude from A on BC is 5cm. Find BC.
Find the length of altitude AD of an isosceles ΔABC in which AB = AC = 2a units and BC = a units.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
In the given figure, D is the midpoint of side BC and AE⊥BC. If BC = a, AC = b, AB = c, AD = p and AE = h, prove that
(i)`B^2=p^2+ax+a^2/x`
(ii)` c^2=p^2-ax+a^2/x`
(iii) `b^2+c^2=2p^2+a^2/2`
(iv)`b^2-c^2=2ax`

State the midpoint theorem
In the given figure, in ∆ABC, point D on side BC is such that, ∠BAC = ∠ADC. Prove that, CA2 = CB × CD
A line is parallel to one side of triangle which intersects remaining two sides in two distinct points then that line divides sides in same proportion.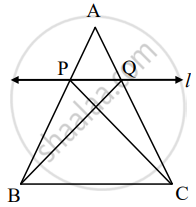
Given: In ΔABC line l || side BC and line l intersect side AB in P and side AC in Q.
To prove: `"AP"/"PB" = "AQ"/"QC"`
Construction: Draw CP and BQ
Proof: ΔAPQ and ΔPQB have equal height.
`("A"(Δ"APQ"))/("A"(Δ"PQB")) = (["______"])/"PB"` .....(i)[areas in proportion of base]
`("A"(Δ"APQ"))/("A"(Δ"PQC")) = (["______"])/"QC"` .......(ii)[areas in proportion of base]
ΔPQC and ΔPQB have [______] is common base.
Seg PQ || Seg BC, hence height of ΔAPQ and ΔPQB.
A(ΔPQC) = A(Δ______) ......(iii)
`("A"(Δ"APQ"))/("A"(Δ"PQB")) = ("A"(Δ "______"))/("A"(Δ "______"))` ......[(i), (ii), and (iii)]
`"AP"/"PB" = "AQ"/"QC"` .......[(i) and (ii)]
In the given figure ΔABC ~ ΔPQR, PM is median of ΔPQR. If ar ΔABC = 289 cm², BC = 17 cm, MR = 6.5 cm then the area of ΔPQM is ______.
 |
 |
Construct an equilateral triangle of side 7 cm. Now, construct another triangle similar to the first triangle such that each of its sides are `5/7` times of the corresponding sides of the first triangle.
Prove that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. In the figure, find EC if `(AD)/(DB) = (AE)/(EC)` using the above theorem.

State and prove Basic Proportionality theorem.
