Advertisements
Advertisements
प्रश्न
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 2cm, AD = 8cm, AE = 12 cm and AC = l8cm.
उत्तर
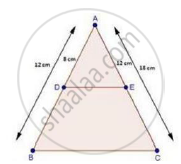
AB = 12 cm, AD = 12 cm and AC = 18 cm.
∴ DB = AB – AD
= 12 – 8
⇒ DB = 4 cm
And, EC = AC – AE
= 18 – 12
⇒ EC = 6 cm
Now, `"AD"/"DB"=8/4=2/1` [∵ DB = 4 cm]
And, `"AE"/"EC"=12/6=2/1` [∵ EC = 6 cm]
`rArr"AD"/"DB"="AE"/"EC"`
Thus, DE divides sides AB and AC of ΔABC in the same ratio.
Therefore, by the converse of basic proportionality theorem,
We have, DE || BC
APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4, AE = 8, DB = x – 4, and EC = 3x – 19, find x.
If D and E are points on sides AB and AC respectively of a ΔABC such that DE || BC and BD = CE. Prove that ΔABC is isosceles.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If `(AD)/(DB) = 4/7` and AC = 6.6cm, find AE.
In the given figure, ABCD is a trapezium in which AB║DC and its diagonals intersect at O. If AO = (5x – 7), OC = (2x + 1) , BO = (7x – 5) and OD = (7x + 1), find the value of x.

ΔABC is am equilateral triangle of side 2a units. Find each of its altitudes.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
ABC is an isosceles triangle, right-angled at B. Similar triangles ACD and ABE are constructed on sides AC and AB. Find the ratio between the areas of ΔABE and ΔACD.
State and converse of Thale’s theorem.
State the midpoint theorem
In fig., line BC || line DE, AB = 2, BD = 3, AC = 4 and CE = x, then find the value of x
