Advertisements
Advertisements
प्रश्न
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 5.6cm, AD = 1.4cm, AC= 7.2 cm and AE = 1.8 cm.
उत्तर
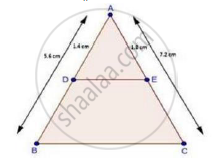
We have,
AB = 5.6 cm, AD = 1.4 cm, AC = 7.2 cm and AE = 1.8 cm
∴ DB = AB – AD
= 5.6 – 1.4
⇒ DB = 4.2 cm
And, EC = AC – AE
= 7.2 – 1.8
⇒ EC = 5.4 cm
Now, `"AD"/"DB"=1.4/4.2=1/3` [∵ DB = 4.2 cm]
And, `"AE"/"EC"=1.8/5.4=1/3` [∵ EC = 5.4 cm]
Thus, DE divides sides AB and AC of ΔABC in the same ratio.
Therefore, by the converse of basic proportionality theorem,
We have, DE || BC
APPEARS IN
संबंधित प्रश्न
In a ΔABC, P and Q are points on sides AB and AC respectively, such that PQ || BC. If AP = 2.4 cm, AQ = 2 cm, QC = 3 cm and BC = 6 cm, find AB and PQ.
M and N are points on the sides PQ and PR respectively of a ΔPQR. For the following case, state whether MN || QR
PM = 4cm, QM = 4.5 cm, PN = 4 cm and NR = 4.5 cm
ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that CQ = `1/4` AC. If PQ produced meets BC at R, prove that R is the midpoint of BC.

In the given figure, O is a point inside a ΔPQR such that ∠PQR such that ∠POR = 90°, OP = 6cm and OR = 8cm. If PQ = 24cm and QR = 26cm, prove that ΔPQR is right-angled.
Find the height of an equilateral triangle of side 12cm.
In the given figure, ∠ACB 90° CD ⊥ AB Prove that `(BC^2)/(AC^2)=(BD)/(AD)`

State the midpoint theorem
In triangle BMP and CNR it is given that PB= 5 cm, MP = 6cm BM = 9 cm and NR = 9cm. If ΔBMP∼ ΔCNR then find the perimeter of ΔCNR
In fig., line BC || line DE, AB = 2, BD = 3, AC = 4 and CE = x, then find the value of x
Construct an equilateral triangle of side 7 cm. Now, construct another triangle similar to the first triangle such that each of its sides are `5/7` times of the corresponding sides of the first triangle.
