Advertisements
Advertisements
प्रश्न
In triangle BMP and CNR it is given that PB= 5 cm, MP = 6cm BM = 9 cm and NR = 9cm. If ΔBMP∼ ΔCNR then find the perimeter of ΔCNR
उत्तर
When two triangles are similar, then the ratios of the lengths of their corresponding sides are proportional.
Here, ΔBMP ~ ΔCNR
∴` (BM)/(CN)=(BP)/(CR)=(MP)/(NR)` ...........(1)
NOW`(BM)/(CN)=(MP)/(NR)` [𝑈𝑠𝑖𝑛𝑔 (1)]
⇒ `CN=(BMxxNR)/(MP)=(9xx9)/6=13.5 cm`
𝐴𝑔𝑎𝑖𝑛, `(BM)/(CN)=(BP)/(CR)` [𝑈𝑠𝑖𝑛𝑔 (1)]
⇒ `CR=(BPxxCN)/(BM)=(5xx13.5)/9=7.5 cm`
Perimeter of ΔCNR = CN + NR + CR = 13.5 + 9 + 7.5 = 30 cm
APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4, AE = 8, DB = x – 4, and EC = 3x – 19, find x.
D and E are the points on the sides AB and AC respectively of a ΔABC such that: AD = 8 cm, DB = 12 cm, AE = 6 cm and CE = 9 cm. Prove that BC = 5/2 DE.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = 4cm, DB = (x – 4) cm, AE = 8cm and EC = (3x – 19) cm.
ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that CQ = `1/4` AC. If PQ produced meets BC at R, prove that R is the midpoint of BC.

Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
In fig, seg DE || sec BC, identify the correct statement.

Find the value of x for which DE || AB in figure.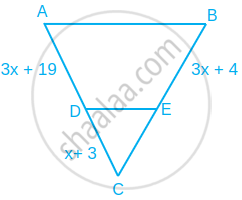
Construct an equilateral triangle of side 7 cm. Now, construct another triangle similar to the first triangle such that each of its sides are `5/7` times of the corresponding sides of the first triangle.
In the given figure, Sand Tare points on sides PQ and PR, respectively of ΔPQR such that ST is parallel to QR and SQ = TR. Prove that ΔPQR is an isosceles triangles.
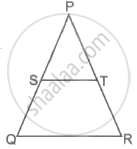
Prove that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. In the figure, find EC if `(AD)/(DB) = (AE)/(EC)` using the above theorem.

