Advertisements
Advertisements
प्रश्न
Each of the equal sides of an isosceles triangle is 25 cm. Find the length of its altitude if the base is 14 cm.
उत्तर
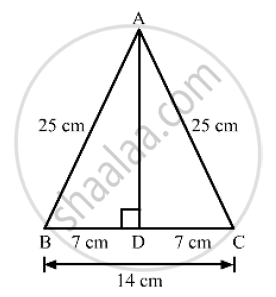
We know that the altitude drawn from the vertex opposite to the non-equal side bisects the non-equal side.
Suppose ABC is an isosceles triangle having equal sides AB and BC.
So, the altitude drawn from the vertex will bisect the opposite side.
Now, In right triangle ABD
By using Pythagoras theorem, we have
`AB^2=BD^2+DA^2`
⇒ `25^2=7^2+DA^2`
⇒ `DA^2=625-49`
⇒ `DA^2=576`
⇒ `DA=24 cm`
APPEARS IN
संबंधित प्रश्न
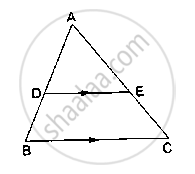
In the following figure, DE || AC and DF || AE. Prove that `("BF")/("FE") = ("BE")/("EC")`

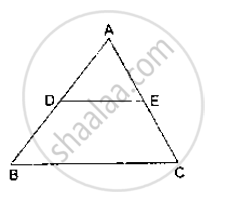
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 2cm, AD = 8cm, AE = 12 cm and AC = l8cm.
M and N are points on the sides PQ and PR respectively of a ΔPQR. For the following case, state whether MN || QR
PM = 4cm, QM = 4.5 cm, PN = 4 cm and NR = 4.5 cm
D and E are the points on the sides AB and AC respectively of a ΔABC such that: AD = 8 cm, DB = 12 cm, AE = 6 cm and CE = 9 cm. Prove that BC = 5/2 DE.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If` (AD)/(AB) = 8/15 and EC = 3.5cm`, find AE.
In the adjoining figure, ABC is a triangle in which AB = AC. IF D and E are points on AB and AC respectively such that AD = AE, show that the points B, C, E and D are concyclic.
In the given figure, O is a point inside a ΔPQR such that ∠PQR such that ∠POR = 90°, OP = 6cm and OR = 8cm. If PQ = 24cm and QR = 26cm, prove that ΔPQR is right-angled.
In figure, PA, QB, RC and SD are all perpendiculars to a line l, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ, QR and RS.
In the given figure, DE || BC. If AD = 3 cm, AB = 7 cm and EC = 3 cm, then the length of AE is ______.
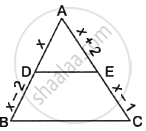
In the given figure, ABC is a triangle in which DE||BC. If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, then find the value of x.