Advertisements
Advertisements
प्रश्न
D and E are the points on the sides AB and AC respectively of a ΔABC such that: AD = 8 cm, DB = 12 cm, AE = 6 cm and CE = 9 cm. Prove that BC = 5/2 DE.
उत्तर
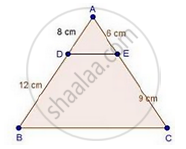
We have,
`"AD"/"DB"=8/12=2/3`
And, `"AE"/"EC"=6/9=2/3`
Since, `"AD"/"DB"="AE"/"EC"`
Then, by converse of basic proportionality theorem
DE || BC
In ΔADE and ΔABC
∠A = ∠A [Common]
∠ADE = ∠B [Corresponding angles]
Then, ΔADE ~ ΔABC [By AA similarity]
`therefore"AD"/"AB"="DE"/"BC"` [Corresponding parts of similar Δ are proportional]
`rArr8/20="DE"/"BC"`
`rArr2/5="DE"/"BC"`
`"BC"=5/2" DE"`
APPEARS IN
संबंधित प्रश्न
In the following figure, DE || AC and DF || AE. Prove that `("BF")/("FE") = ("BE")/("EC")`

In the given figure, PS is the bisector of ∠QPR of ΔPQR. Prove that `(QS)/(SR) = (PQ)/(PR)`

In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8cm, AB = 12 cm and AE = 12 cm, find CE.
Two vertical poles of height 9m and 14m stand on a plane ground. If the distance between their feet is 12m, find the distance between their tops.
A guy wire attached to a vertical pole of height 18 m is 24m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
State the midpoint theorem
In the given figure, in ∆ABC, point D on side BC is such that, ∠BAC = ∠ADC. Prove that, CA2 = CB × CD
In fig, seg DE || sec BC, identify the correct statement.

Construct an equilateral triangle of side 7 cm. Now, construct another triangle similar to the first triangle such that each of its sides are `5/7` times of the corresponding sides of the first triangle.
State and prove Basic Proportionality theorem.
