Advertisements
Advertisements
प्रश्न
D and E are the points on the sides AB and AC respectively of a ΔABC such that: AD = 8 cm, DB = 12 cm, AE = 6 cm and CE = 9 cm. Prove that BC = 5/2 DE.
उत्तर
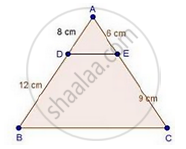
We have,
`"AD"/"DB"=8/12=2/3`
And, `"AE"/"EC"=6/9=2/3`
Since, `"AD"/"DB"="AE"/"EC"`
Then, by converse of basic proportionality theorem
DE || BC
In ΔADE and ΔABC
∠A = ∠A [Common]
∠ADE = ∠B [Corresponding angles]
Then, ΔADE ~ ΔABC [By AA similarity]
`therefore"AD"/"AB"="DE"/"BC"` [Corresponding parts of similar Δ are proportional]
`rArr8/20="DE"/"BC"`
`rArr2/5="DE"/"BC"`
`"BC"=5/2" DE"`
APPEARS IN
संबंधित प्रश्न
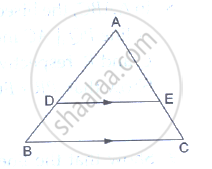
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 2cm, AD = 8cm, AE = 12 cm and AC = l8cm.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 10.8 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = 4cm, DB = (x – 4) cm, AE = 8cm and EC = (3x – 19) cm.
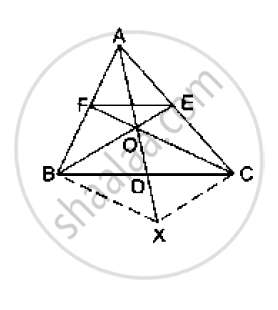
In the given figure, side BC of a ΔABC is bisected at D
and O is any point on AD. BO and CO produced meet
AC and AB at E and F respectively, and AD is
produced to X so that D is the midpoint of OX.
Prove that AO : AX = AF : AB and show that EF║BC.
A guy wire attached to a vertical pole of height 18 m is 24m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
ΔABC is am equilateral triangle of side 2a units. Find each of its altitudes.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
In ΔABC, AB = 6 cm and DE || BC such that AE = `1/4` AC then the length of AD is ______.
In the given figure ΔABC ~ ΔPQR, PM is median of ΔPQR. If ar ΔABC = 289 cm², BC = 17 cm, MR = 6.5 cm then the area of ΔPQM is ______.
 |
 |
In the given figure, PQ || AC. If BP = 4 cm, AP = 2.4 cm and BQ = 5 cm, then length of BC is ______.

