Question

State and prove Basic Proportionality theorem.

Answer 1

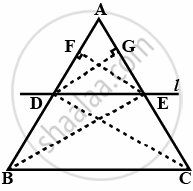
Basic Proportionality Theorem states that, if a line is parallel to a side of a triangle which intersects the other sides into two distinct points, then the line divides those sides of the triangle in proportion.

Let ABC be the triangle.

The line 1 parallel to BC intersect AB at D and AC at E.

To prove `(AD)/(DB) = (AE)/(EC)`

Join BE, CD

Draw EF ⊥ AB, DG ⊥ CA

Since EF ⊥ AB,

EF is the height of triangles ADE and DBE

Area of ΔADE = `1/2 xx "base" xx "height"`

= `1/2 AD xx EF`

Area of ΔDBE = `1/2 xx DB xx EF`

`("Area of"  ΔADE)/("Area of"  ΔDBE) = (1/2 xx AD xx  EF)/(1/2 xx DB xx EF) = (AD)/(DB)`  ...(1)

Similarly,

`("Area of"  ΔADE)/("Area of"  ΔDCE) = (1/2 xx AE xx  DG)/(1/2 xx EC xx DG) = (AE)/(EC)`  ...(2)

But ΔDBE and ΔDCE are the same base DE and between the same parallel straight line BC and DE.

Area of ΔDBE = Area of ΔDCE  ...(3)

From (1), (2) and (3), we have

`(AD)/(DB) = (AE)/(EC)`

Hence proved.