Advertisements
Advertisements
प्रश्न
Draw an isosceles triangle with base 5 cm and height 4 cm. Draw a triangle similar to the triangle drawn whose sides are `2/3` times the sides of the triangle.
उत्तर

APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 2 cm, AB = 6 cm and AC = 9 cm, find AE.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"BD"=4/5` and EC = 2.5 cm, find AE
In three line segments OA, OB, and OC, points L, M, N respectively are so chosen that LM || AB and MN || BC but neither of L, M, N nor of A, B, C are collinear. Show that LN ||AC.
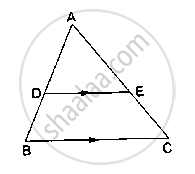
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If AB = 13.3cm, AC = 11.9cm and EC = 5.1cm, find AD.
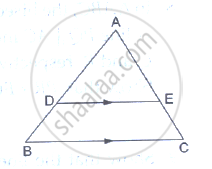
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = 4cm, DB = (x – 4) cm, AE = 8cm and EC = (3x – 19) cm.
ΔABC and ΔDBC lie on the same side of BC, as shown in the figure. From a point P on BC, PQ||AB and PR||BD are drawn, meeting AC at Q and CD at R respectively. Prove that QR||AD.
ΔABC is an isosceles triangle with AB = AC = 13cm. The length of altitude from A on BC is 5cm. Find BC.
ΔABC is am equilateral triangle of side 2a units. Find each of its altitudes.
Find the height of an equilateral triangle of side 12cm.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
In a ABC , AD is a median and AL ⊥ BC .
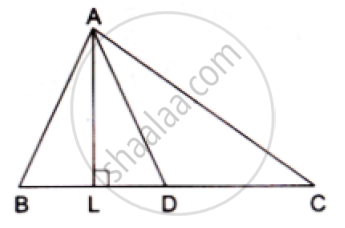
Prove that
(a) `AC^2=AD^2+BC DL+((BC)/2)^2`
(b) `AB^2=AD^2-BC DL+((BC)/2)^2`
(c) `AC^2+AB^2=2.AD^2+1/2BC^2`
A line is parallel to one side of triangle which intersects remaining two sides in two distinct points then that line divides sides in same proportion.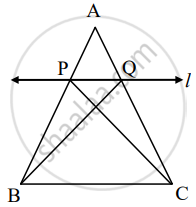
Given: In ΔABC line l || side BC and line l intersect side AB in P and side AC in Q.
To prove: `"AP"/"PB" = "AQ"/"QC"`
Construction: Draw CP and BQ
Proof: ΔAPQ and ΔPQB have equal height.
`("A"(Δ"APQ"))/("A"(Δ"PQB")) = (["______"])/"PB"` .....(i)[areas in proportion of base]
`("A"(Δ"APQ"))/("A"(Δ"PQC")) = (["______"])/"QC"` .......(ii)[areas in proportion of base]
ΔPQC and ΔPQB have [______] is common base.
Seg PQ || Seg BC, hence height of ΔAPQ and ΔPQB.
A(ΔPQC) = A(Δ______) ......(iii)
`("A"(Δ"APQ"))/("A"(Δ"PQB")) = ("A"(Δ "______"))/("A"(Δ "______"))` ......[(i), (ii), and (iii)]
`"AP"/"PB" = "AQ"/"QC"` .......[(i) and (ii)]
From fig., seg PQ || side BC, AP = x + 3, PB = x – 3, AQ = x + 5, QC = x – 2, then complete the activity to find the value of x.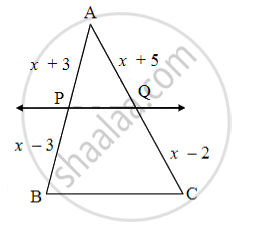
In ΔPQB, PQ || side BC
`"AP"/"PB" = "AQ"/(["______"])` ...[______]
`(x + 3)/(x - 3) = (x + 5)/(["______"])`
(x + 3) [______] = (x + 5)(x – 3)
x2 + x – [______] = x2 + 2x – 15
x = [______]
ΔABC ~ ΔDEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, then the perimeter of ΔDEF is ______.
In the given figure ΔABC ~ ΔPQR, PM is median of ΔPQR. If ar ΔABC = 289 cm², BC = 17 cm, MR = 6.5 cm then the area of ΔPQM is ______.
 |
 |
ABCD is a trapezium in which AB || DC and P and Q are points on AD and BC, respectively such that PQ || DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD.
O is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB || DC. Through O, a line segment PQ is drawn parallel to AB meeting AD in P and BC in Q. Prove that PO = QO.
Prove that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. In the figure, find EC if `(AD)/(DB) = (AE)/(EC)` using the above theorem.

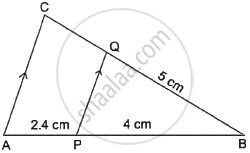
In the given figure, PQ || AC. If BP = 4 cm, AP = 2.4 cm and BQ = 5 cm, then length of BC is ______.