Advertisements
Advertisements
प्रश्न
O is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB || DC. Through O, a line segment PQ is drawn parallel to AB meeting AD in P and BC in Q. Prove that PO = QO.
उत्तर
Given ABCD is a trapezium.
Diagonals AC and BD are intersect at O.
PQ || AB || DC
To prove: PO = QO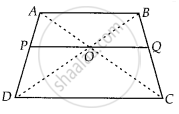
Proof: In ∆ABD and ∆POD,
PO || AB ...[∵ PQ || AB]
∠D = ∠D ...[Common angle]
∠ABD = ∠POD ...[Corresponding angles]
∴ ∆ABD ~ ∆POD ...[By AAA similarity criterion]
Then, `("OP")/("AB") = ("PD")/("AD")` ...(i)
In ∆ABC and ∆OQC,
OQ || AB ...[∵ OQ || AB]
∠C = ∠C ...[Common angle]
∠BAC = ∠QOC ...[Corresponding angles]
∴ ∆ABC ~ ∆OQC ...[By AAA similarity criterion]
Then, `("OQ")/("AB") = ("QC")/("BC")` ...(ii)
Now, In ∆ADC,
OP || DC
∴ `("AP")/("PD") = ("OA")/("OC")` [By basic proportionality theorem] ...(iii)
In ∆ABC,
OQ || AB
∴ `("BQ")/("QC") = ("OA")/("OC")` [By basic proportionality theorem] ...(iv)
From equations (iii) and (iv), we get
`("AP")/("PD") = ("BQ")/("QC")`
Adding 1 on both sides, we get
`("AP")/("PD") + 1 = ("BQ")/("QC") + 1`
⇒ `("AP" + "PD")/("PD") = ("BQ" + "QC")/("QC")`
⇒ `("AD")/("PD") = ("BC")/("QC")`
⇒ `("PD")/("AD") = ("QC")/("BC")`
⇒ `("OP")/("AB") = ("OQ")/("BC")` ...[From equations (i) and (ii)]
⇒ `("OP")/("AB") = ("OQ")/("AB")` ...[From equation (ii)]
⇒ OP = OQ
Hence proved.
APPEARS IN
संबंधित प्रश्न
In the following figure, DE || AC and DF || AE. Prove that `("BF")/("FE") = ("BE")/("EC")`

In the given figure, PS is the bisector of ∠QPR of ΔPQR. Prove that `(QS)/(SR) = (PQ)/(PR)`

In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 6 cm, DB = 9 cm and AE = 8 cm, find AC.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8cm, AB = 12 cm and AE = 12 cm, find CE.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = 4cm, DB = (x – 4) cm, AE = 8cm and EC = (3x – 19) cm.
ΔABC is am equilateral triangle of side 2a units. Find each of its altitudes.
Find the length of a diagonal of a rectangle whose adjacent sides are 30cm and 16cm.
In the given figure, D is the midpoint of side BC and AE⊥BC. If BC = a, AC = b, AB = c, AD = p and AE = h, prove that
(i)`B^2=p^2+ax+a^2/x`
(ii)` c^2=p^2-ax+a^2/x`
(iii) `b^2+c^2=2p^2+a^2/2`
(iv)`b^2-c^2=2ax`

ΔABC ~ ΔDEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, then the perimeter of ΔDEF is ______.
Construct an equilateral triangle of side 7 cm. Now, construct another triangle similar to the first triangle such that each of its sides are `5/7` times of the corresponding sides of the first triangle.
