Advertisements
Advertisements
प्रश्न
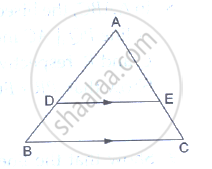
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = 4cm, DB = (x – 4) cm, AE = 8cm and EC = (3x – 19) cm.
उत्तर
In Δ ABC, it is given that DE ‖ BC.
Applying Thales’ theorem, we have :
`(AD)/(DB) = (AE)/(EC)`
⟹ `4/(x-4) = 8 /(3x -19)`
⟹ 4 (3x-19) = 8 (x-4)
⟹ 12x – 76 = 8x – 32
⟹ 4x = 44
⟹ x = 11 cm
APPEARS IN
संबंधित प्रश्न
In the following figure, DE || AC and DF || AE. Prove that `("BF")/("FE") = ("BE")/("EC")`

In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"BD"=4/5` and EC = 2.5 cm, find AE
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8x − 7, DB = 5x − 3, AE = 4x − 3 and EC = (3x − 1), find the value of x.
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC.
If `(AD)/(DB) = 4/7` and AC = 6.6cm, find AE.
In the given figure, ABCD is a trapezium in which AB║DC and its diagonals intersect at O. If AO = (5x – 7), OC = (2x + 1) , BO = (7x – 5) and OD = (7x + 1), find the value of x.

ΔABC and ΔDBC lie on the same side of BC, as shown in the figure. From a point P on BC, PQ||AB and PR||BD are drawn, meeting AC at Q and CD at R respectively. Prove that QR||AD.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
State the basic proportionality theorem.
In triangle BMP and CNR it is given that PB= 5 cm, MP = 6cm BM = 9 cm and NR = 9cm. If ΔBMP∼ ΔCNR then find the perimeter of ΔCNR
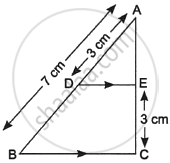
In the given figure, DE || BC. If AD = 3 cm, AB = 7 cm and EC = 3 cm, then the length of AE is ______.