Advertisements
Advertisements
Question
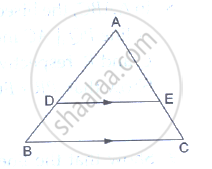
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC. Find the value of x, when
AD = 4cm, DB = (x – 4) cm, AE = 8cm and EC = (3x – 19) cm.
Solution
In Δ ABC, it is given that DE ‖ BC.
Applying Thales’ theorem, we have :
`(AD)/(DB) = (AE)/(EC)`
⟹ `4/(x-4) = 8 /(3x -19)`
⟹ 4 (3x-19) = 8 (x-4)
⟹ 12x – 76 = 8x – 32
⟹ 4x = 44
⟹ x = 11 cm
APPEARS IN
RELATED QUESTIONS
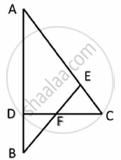
In the given figure, D is a point on side BC of ΔABC such that ∠ADC=∠BAC . Prove that AD is the bisector of ∠BAC.
In a ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 10.8 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm.
If D and E are points on sides AB and AC respectively of a ΔABC such that DE || BC and BD = CE. Prove that ΔABC is isosceles.
In the given figure, O is a point inside a ΔPQR such that ∠PQR such that ∠POR = 90°, OP = 6cm and OR = 8cm. If PQ = 24cm and QR = 26cm, prove that ΔPQR is right-angled.
Find the length of altitude AD of an isosceles ΔABC in which AB = AC = 2a units and BC = a units.
ABC is an isosceles triangle, right-angled at B. Similar triangles ACD and ABE are constructed on sides AC and AB. Find the ratio between the areas of ΔABE and ΔACD.
State and converse of Thale’s theorem.
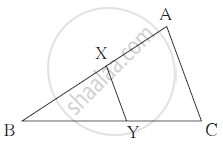
In the adjoining figure,
seg XY || seg AC, If 3AX = 2BX
and XY = 9 then find the length of AC.
Draw an isosceles triangle with base 5 cm and height 4 cm. Draw a triangle similar to the triangle drawn whose sides are `2/3` times the sides of the triangle.
In the given figure ∠CEF = ∠CFE. F is the midpoint of DC. Prove that `(AB)/(BD) = (AE)/(FD)`